题目内容
定义在R上的函数 ,
,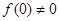 ,当
,当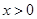 时,
时,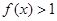 ,且对任意实数
,且对任意实数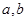 ,
,
有 ,
,
求证: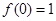 ;
;
(2)证明: 是R上的增函数;
是R上的增函数;
(3)若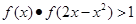 ,求
,求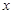 的取值范围。
的取值范围。
(1)a=b=0,得f(0)=1。
(2)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0
利用 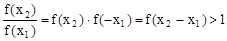 得到 f(x2)>f(x1) 。
得到 f(x2)>f(x1) 。
(3)0<x<3
解析试题分析:(1)令a=b=0,则f(0)=[f(0)]2∵ f(0)≠0 ∴ f(0)=1 4
(2)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0
∴ 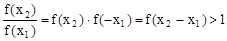 ∴ f(x2)>f(x1) ∴ f(x)在R上是增函数
∴ f(x2)>f(x1) ∴ f(x)在R上是增函数
8
(3)f(x)·f(2x-x2)=f[x+(2x-x2)]=f(-x2+3x) 又1=f(0),f(x)在R上递增
∴ 由f(3x-x2)>f(0)得:x-x2>0 ∴ 0<x<3 12
考点:函数的单调性,抽象函数不等式的解法,一元二次不等式的解法,赋值法。
点评:中档题,本题作为一道“连环题”,可采用分步得分的原则,首先利用“赋值法”解题。本题主要难点是配凑 。抽象函数不等式的解法,主要是利用函数的单调性,转化成具体不等式求解。
。抽象函数不等式的解法,主要是利用函数的单调性,转化成具体不等式求解。

练习册系列答案
相关题目
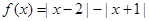 .
.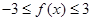 ;
;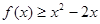
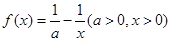
 在
在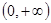 上的单调;
上的单调;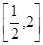 上的值域是
上的值域是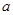 的值.
的值.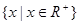 ,且f(x)为增函数,f(xy)=f(x)+f(y)。
,且f(x)为增函数,f(xy)=f(x)+f(y)。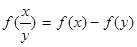 ;
;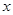 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米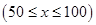 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油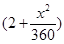 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.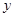 关于
关于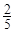 小时,种植一捆沙棘树苗用时
小时,种植一捆沙棘树苗用时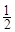 小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
小时.应如何分配A,B两组的人数,使植树活动持续时间最短?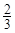 小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.