题目内容
9.对于函数f(x)=tan2x,下列选项中正确的是( )| A. | f(x)在(-$\frac{π}{2}$,$\frac{π}{4}$)上是递增的 | B. | f(x)在定义域上单调递增 | ||
| C. | f(x)的最小正周期为π | D. | f(x)的所有对称中心为($\frac{kπ}{4}$,0) |
分析 求出函数的周期,判断A、C的正误;正切函数的单调性判断B的正误;求出对称中心判断D的正误;
解答 解:x=-$\frac{π}{4}$时,函数没有意义,A不正确;
正切函数在定义域上不是单调函数,B不正确;
函数f(x)=tan2x的周期为:$\frac{π}{2}$,所以C不正确;
($\frac{kπ}{4}$,0)是函数的对称中心,所以D正确.
故选:D.
点评 本题考查正弦函数的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
17. 如图是正方体平面展开图,在这个正方体中①BM∥平面ED;②CN与BE是异面直线;③CN与BM成60°角;④DC与BN垂直⑤平面BDM∥平面AFN
如图是正方体平面展开图,在这个正方体中①BM∥平面ED;②CN与BE是异面直线;③CN与BM成60°角;④DC与BN垂直⑤平面BDM∥平面AFN
以上五个命题中,正确命题的个数是( )
 如图是正方体平面展开图,在这个正方体中①BM∥平面ED;②CN与BE是异面直线;③CN与BM成60°角;④DC与BN垂直⑤平面BDM∥平面AFN
如图是正方体平面展开图,在这个正方体中①BM∥平面ED;②CN与BE是异面直线;③CN与BM成60°角;④DC与BN垂直⑤平面BDM∥平面AFN 以上五个命题中,正确命题的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
4.下列函数中,在区间[0,2]上是增函数的是( )
| A. | y=x2-4x+5 | B. | y=log${\;}_{\frac{1}{2}}$x | C. | y=2-x | D. | y=$\sqrt{x}$ |
1.下列四组函数中,表示同一函数的是( )
| A. | f(x)=log22x,g(x)=$\root{3}{{x}^{3}}$ | B. | f(x)=$\sqrt{{x}^{2}}$,g(x)=x | ||
| C. | f(x)=x,g(x)=$\frac{{x}^{2}}{x}$ | D. | f(x)=lnx2,g(x)=2lnx |
19. 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图,且过点$A(\frac{7π}{12},0),B(0,-1)$,则以下结论不正确的是( )
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图,且过点$A(\frac{7π}{12},0),B(0,-1)$,则以下结论不正确的是( )
 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图,且过点$A(\frac{7π}{12},0),B(0,-1)$,则以下结论不正确的是( )
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的部分图象如图,且过点$A(\frac{7π}{12},0),B(0,-1)$,则以下结论不正确的是( )| A. | f(x)的图象关于直线$x=-\frac{π}{6}$ 对称 | B. | f(x)的图象关于点$(\frac{π}{12},0)$对称 | ||
| C. | f(x) 在$[-\frac{π}{2},-\frac{π}{3}]$ 上是增函数 | D. | f(x) 在$[\frac{4π}{3},\frac{3π}{2}]$ 上是减函数 |
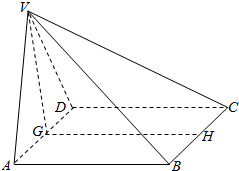 在四棱锥中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD,G、H分别为AD、BC中点.证明:
在四棱锥中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD,G、H分别为AD、BC中点.证明: