题目内容
19.已知f(x)=$\frac{{2}^{x}+a}{{2}^{x}-1}$.(1)求函数定义域;
(2)若f(x)为奇函数,求实数a的值;
(3)在(2)的条件下利用定义证明:f(x)在(0,+∞)为减函数.
分析 (1)根据分母不等0,求出x的范围,可得函数的定义域;
(2)根据f(x)为奇函数,f(-x)=-f(x)恒成立,代入特殊值,可得实数a的值;
(3)设x1,x2∈(-∞,0)且x1<x2,结合对数函数的图象和性质,判断f(x1),f(x2)的大小,结合函数单调性的定义,可得答案.
解答 解:(1)由2x-1≠0得:x≠0,
故函数f(x)=$\frac{{2}^{x}+a}{{2}^{x}-1}$的定义域为{x|x≠0};
(2)若f(x)为奇函数,
则f(-1)=-f(1),
即$\frac{\frac{1}{2}+a}{\frac{1}{2}-1}$=-$\frac{2+a}{2-1}$,
解得:a=1,
经检验当a=1时,f(-x)=-f(x)恒成立,满足f(x)为奇函数;
(3)设x1,x2∈(-∞,0)且x1<x2,
则${2}^{{x}_{1}}-1$<0,${2}^{{x}_{2}}-1<0$,${2}^{{x}_{2}}{-2}^{{x}_{1}}>0$
∴f(x1)-f(x2)=$\frac{{2}^{{x}_{1}}+1}{{2}^{{x}_{1}}-1}$-$\frac{{2}^{{x}_{2}}+1}{{2}^{{x}_{2}}-1}$=$\frac{{2({2}^{{x}_{2}}-2}^{{x}_{1}})}{{(2}^{{x}_{1}}-1)({2}^{{x}_{2}}-1)}$>0,
∴f(x1)>f(x2).
根据函数单调性的定义知函数f(x)在(-∞,0)上为减函数
点评 本题考查的知识点是函数的定义域,函数的单调性,函数的奇偶性,是函数图象和性质的综合应用.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
10.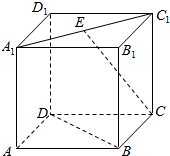 如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
 如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
8.若一个底面是正三角形的三棱柱的正视图如图所示,则体积等于( )
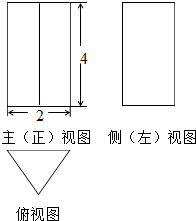

| A. | 4$\sqrt{3}$ | B. | $\frac{4}{3}$$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{3}$ |
9.对于函数f(x)=tan2x,下列选项中正确的是( )
| A. | f(x)在(-$\frac{π}{2}$,$\frac{π}{4}$)上是递增的 | B. | f(x)在定义域上单调递增 | ||
| C. | f(x)的最小正周期为π | D. | f(x)的所有对称中心为($\frac{kπ}{4}$,0) |