题目内容
4．下列函数中，在区间[0，2]上是增函数的是（ ）| A． | y=x2-4x+5 | B． | y=log${\;}_{\frac{1}{2}}$x | C． | y=2-x | D． | y=$\sqrt{x}$ |
分析 利用二次函数性质，对数函数，指数函数以及底数函数的性质判断即可．
解答 解：A、y=x2-4x+4+1=（x-2）2+1，在区间[0，2]上是减函数；
B、y=log${\;}_{\frac{1}{2}}$x，在区间[0，2]上是减函数；
C、y=2-x，在区间[0，2]上是减函数；
D、y=$\sqrt{x}$，在区间[0，2]上是增函数，
故选：D．
点评 此题考查了函数单调性的判断与证明，熟练掌握各函数的单调性是解本题的关键．
练习册系列答案
53随堂测系列答案
相关题目
15．已知P（t，3t），t∈R，M是圆O1：（x+2）2+y2=$\frac{1}{4}$上的动点，N是O2：（x-4）2+y2=$\frac{1}{4}$上的动点，则|PN|-|PM|的最大值是（ ）
| A． | $\frac{3\sqrt{5}}{5}$+1 | B． | $\frac{3\sqrt{5}}{5}-1$ | C． | $\frac{6\sqrt{5}}{5}$+1 | D． | $\frac{6\sqrt{5}}{5}$ |
12．若角α的终边过点（-1，2），则cos（π-2α）的值为（ ）
| A． | $\frac{3}{5}$ | B． | -$\frac{3}{5}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | -$\frac{\sqrt{5}}{5}$ |
19．如果一个点是一个指数函数的图象与一个对数函数的图象的公共点，那么称这个点为“好点”，在下面的六个点M（1，1）、N（1，2）、P（1，3）、Q（2，1）、R（2，2）、T（2，3）中，“好点”的个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
9．对于函数f（x）=tan2x，下列选项中正确的是（ ）
| A． | f（x）在（-$\frac{π}{2}$，$\frac{π}{4}$）上是递增的 | B． | f（x）在定义域上单调递增 | ||
| C． | f（x）的最小正周期为π | D． | f（x）的所有对称中心为（$\frac{kπ}{4}$，0） |
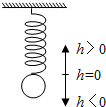如图，挂在下方的小球做上下运动，小球在t（s）时相对于平衡位置（即静止的位置）的高度为h（单位：cm），由下列关系式确定：h=2sin（t+$\frac{π}{4}$），t∈[0，+∞）．
14．设命题p：“?x＞1，x2≥x，则其否定非p为（ ）
| A． | ?x＞1，x2≤x | B． | $?{x}_{0}＞1，{x}_{0}^{2}＞{x}_{0}$ | ||
| C． | $?{x}_{0}≤1，{x}_{0}^{2}≤{x}_{0}$ | D． | $?{x}_{0}＞1，{x}_{0}^{2}＜{x}_{0}$ |