题目内容
20.在平面直角坐标系中,点P($\frac{1}{2}$,$\frac{2}{3}$)在角α的终边上,点Q($\frac{1}{3}$,-1)在角β的终边上,点M(sin$\frac{2π}{3}$,cos$\frac{2π}{3}$)在角γ终边上.(1)求sinα,cosβ,tanγ的值;
(2)求sin(α+2β)的值.
分析 由条件利用任意角的三角函数的定义求得sinα,cosβ,tanγ的值,再利用二倍角公式求得sin2β、cos2β的值,再利用两角和的正弦公式求得sin(α+2β)的值.
解答 解:(1)∵点P($\frac{1}{2}$,$\frac{2}{3}$)在角α的终边上,点Q($\frac{1}{3}$,-1)在角β的终边上,
点M(sin$\frac{2π}{3}$,cos$\frac{2π}{3}$)在角γ终边上,
∴sinα=$\frac{\frac{2}{3}}{\sqrt{\frac{1}{4}+\frac{4}{9}}}$=$\frac{4}{5}$,cosα=$\frac{\frac{1}{2}}{\sqrt{\frac{1}{4}+\frac{4}{9}}}$=$\frac{3}{5}$;
sinβ=$\frac{-1}{\sqrt{\frac{1}{9}+1}}$=-$\frac{3\sqrt{10}}{10}$,cosβ=$\frac{\frac{1}{3}}{\sqrt{\frac{1}{9}+1}}$=$\frac{\sqrt{10}}{10}$;
tanγ=$\frac{cos\frac{2π}{3}}{sin\frac{2π}{3}}$=-$\frac{\sqrt{3}}{3}$.
(2)由(1)得 sin2β=2sinβcosβ=-$\frac{3}{5}$<0,cos2β=2cos2β-1=-$\frac{4}{5}$,
∴sin(α+2β)=sinαcos2β+cosαsin2β=-1.
点评 本题主要考查任意角的三角函数的定义、二倍角公式、两角和的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
10.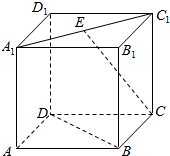 如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
 如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
8.若一个底面是正三角形的三棱柱的正视图如图所示,则体积等于( )
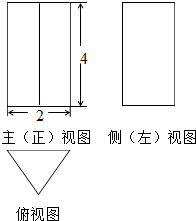

| A. | 4$\sqrt{3}$ | B. | $\frac{4}{3}$$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{3}$ |
15.已知P(t,3t),t∈R,M是圆O1:(x+2)2+y2=$\frac{1}{4}$上的动点,N是O2:(x-4)2+y2=$\frac{1}{4}$上的动点,则|PN|-|PM|的最大值是( )
| A. | $\frac{3\sqrt{5}}{5}$+1 | B. | $\frac{3\sqrt{5}}{5}-1$ | C. | $\frac{6\sqrt{5}}{5}$+1 | D. | $\frac{6\sqrt{5}}{5}$ |
5.已知定义域为R的偶函数f(x)在(0,+∞)上为增函数,则( )
| A. | f(4)>f(3) | B. | f(-5)>f(5) | C. | f(-3)>f(-5) | D. | f(3)>f(-6) |
12.若角α的终边过点(-1,2),则cos(π-2α)的值为( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
9.对于函数f(x)=tan2x,下列选项中正确的是( )
| A. | f(x)在(-$\frac{π}{2}$,$\frac{π}{4}$)上是递增的 | B. | f(x)在定义域上单调递增 | ||
| C. | f(x)的最小正周期为π | D. | f(x)的所有对称中心为($\frac{kπ}{4}$,0) |