题目内容
4.已知函数f(x)=x+a1nx,其中a为常数,且0<a<4.(1)用定义证明:函数g(x)=f(x)+$\frac{1}{x}$-alnx在区间(0,1)上单凋递减;
(2)当a=1时,求f(x)在[e,e2](e=2.71828…)上的值域:
(3)若f(x)≥3e+1在区间[e,e2]上有解,求实数a的取值范围.
分析 (1)化简g(x)=f(x)+$\frac{1}{x}$-alnx=x+$\frac{1}{x}$,从而按定义法的五步骤证明即可;
(2)当a=1时,函数f(x)=x+1nx,求导f′(x)=1+$\frac{1}{x}$>0;从而可得f(e)≤f(x)≤f(e2),从而解得;
(3)令F(x)=f(x)-3e-1=x+a1nx-3e-1,求导F′(x)=1+$\frac{a}{x}$>0;从而可得F(e)•F(e2)≤0,从而解得.
解答 解:(1)证明:g(x)=f(x)+$\frac{1}{x}$-alnx=x+$\frac{1}{x}$,
任取x1,x2∈(0,1),且x1<x2;
则f(x1)-f(x2)=x1+$\frac{1}{{x}_{1}}$-(x2+$\frac{1}{{x}_{2}}$)
=(x1-x2)(1-$\frac{1}{{x}_{1}{x}_{2}}$)
∵0<x1<x2<1,
∴x1-x2<0,1-$\frac{1}{{x}_{1}{x}_{2}}$<0;
故f(x1)-f(x2)>0,
故函数g(x)=f(x)+$\frac{1}{x}$-alnx在区间(0,1)上单凋递减;
(2)当a=1时,函数f(x)=x+1nx,f′(x)=1+$\frac{1}{x}$>0;
故f(x)在[e,e2]上是增函数;
故f(e)≤f(x)≤f(e2),
即e+1≤f(x)≤2+e2,
故f(x)在[e,e2]上的值域为[1+e,2+e2];
(3)令F(x)=f(x)-3e-1=x+a1nx-3e-1,
∵F′(x)=1+$\frac{a}{x}$>0;
故F(x)在区间[e,e2]上单调递增,且F(x)在区间[e,e2]上连续;
故F(e)•F(e2)≤0,
即(a-2e-1)(2a+e2-3e-1)≤0,
解得,$\frac{3e+1-{e}^{2}}{2}$≤a≤2e+1,
故$\frac{3e+1-{e}^{2}}{2}$≤a<4.
点评 本题考查了导数在判断函数的单调性时的应用及函数的零点的判定定理的应用.

| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | b>c>a |
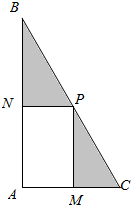 某中学为了落实“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x米,x∈[10,20].
某中学为了落实“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x米,x∈[10,20].