题目内容
19.已知集合M是满足下列性质的函数f(x)的全体:存在非零常数T,使得对任意的实数x,有f(x+T)=Tf(x)成立.(1)证明:f(x)=x2不属于集合M;
(2)设f(x)∈M,且T=2.已知当1<x<2时,f(x)=x+lnx,求当-3<x<-2时,f(x)的解析式.
分析 (1)利用反证法,假设f(x)∈M,则f(x+T)=Tf(x),即(x+T)2=Tx2对任意的x恒成立,推出T无解,即假设不成立,肯定结论.
(2)将-3<x<-2转化为1<x+4<2,利用当1<x<2时,f(x)=x+lnx,即可求得f(x+4)的解析式,再利用f(x+T)=Tf(x),即可求得f(x)的解析式
解答 (1)证明:假设f(x)∈M,则f(x+T)=Tf(x),即(x+T)2=Tx2对任意的x恒成立,
即(1-T)x2+2Tx+T2=0对任意的x恒成立.
∴$\left\{\begin{array}{l}{1-T=0}\\{2T=0}\\{{T}^{2}=0}\end{array}\right.$.
∴T∈∅.
假设错误,所以f(x)=x2不属于集合M.
(2)∵-3<x<-2,
∴1<x+4<2,
∴f(x+4)=x+4+ln(x+4),
∵存在非零常数T,使得对任意x∈R,有f(x+T)=Tf(x)成立,
∴令T=2,
∴f(x+4)=f[(x+2)+2]=2f(x+2)=4f(x),
∴f(x)=$\frac{1}{4}$[x+4+ln(x+4)],
∴当-3<x<-2时,f(x)的解析式是f(x)=$\frac{1}{4}$[x+4+ln(x+4)].
点评 本题考查了抽象函数及其应用,反证法,函数解析式的求解及常用方法,求函数解析式常见的方法有:待定系数法,换元法,凑配法,消元法等.属于中档题

练习册系列答案
相关题目
14.AD、BE分别为△ABC的边BC、AC上的中线,且$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{BE}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$为( )
| A. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$ | D. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$ |
8.设集合A={x|2≤x<4},B={x|3x-7≥8-2x},则A∪B等于( )
| A. | {x|3≤x<4} | B. | {x|x≥3} | C. | {x|x>2} | D. | {x|x≥2} |
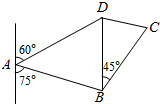 如图所示B岛在A岛南偏东750方向,距离A岛$4\sqrt{3}$海里,A岛观察所发现在B岛正北方向与A岛的北偏东600方向的交点处D有海上非法走私交易活动,A岛观察人员马上通知在B岛东北方向,距离B岛7海里C处的缉私艇在半小时内赶到D处,求缉私艇的速度至少每小时多少海里?
如图所示B岛在A岛南偏东750方向,距离A岛$4\sqrt{3}$海里,A岛观察所发现在B岛正北方向与A岛的北偏东600方向的交点处D有海上非法走私交易活动,A岛观察人员马上通知在B岛东北方向,距离B岛7海里C处的缉私艇在半小时内赶到D处,求缉私艇的速度至少每小时多少海里?