题目内容
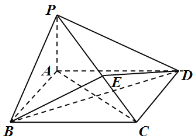
【题目】在棱长AB=AD=2,AA1=3的长方体ABCDA1B1C1D1中,点E是平面BCC1B1上的动点,点F是CD的中点.试确定点E的位置,使D1E⊥平面AB1F.

【答案】见解析
【解析】
分别以AB、AD、AA1为x、y、z轴建立空间直角坐标系如图所示.可得A、B1、D1、F各点的坐标,设E(2,y,z),得出向量![]() 、
、![]() 和
和![]() 的坐标.若D1E⊥平面AB1F,则D1E⊥AB1且D1E⊥AF,利用垂直向量数量积为零的方法建立方程组,解出y=1且z=
的坐标.若D1E⊥平面AB1F,则D1E⊥AB1且D1E⊥AF,利用垂直向量数量积为零的方法建立方程组,解出y=1且z=![]() ,得E(2,1,
,得E(2,1,![]() ),因此可得存在平面BCC1B1上的动点E,当E到BB1和BC的距离分别为1、
),因此可得存在平面BCC1B1上的动点E,当E到BB1和BC的距离分别为1、![]() 时,可使D1E⊥平面AB1F.
时,可使D1E⊥平面AB1F.
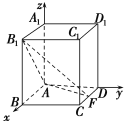
建立空间直角坐标系如图,则A(0,0,0),F(1,2,0),B1(2,0,3),D1(0,2,3),![]() =(1,2,0),
=(1,2,0),![]() =(2,0,3).设E(2,y,z),则
=(2,0,3).设E(2,y,z),则![]() =(2,y-2,z-3).
=(2,y-2,z-3).
∵D1E⊥平面AB1F,
∴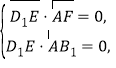 即
即![]() 解得
解得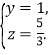
∴E![]() 即为所求.
即为所求.

练习册系列答案
相关题目