题目内容
【题目】已知圆F1:(x+1)2+y2=1,圆F2:(x﹣1)2+y2=25,动圆P与圆F1外切并且与圆F2内切,动圆圆心P的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)若曲线C与x轴的交点为A1 , A2 , 点M是曲线C上异于点A1 , A2的点,直线A1M与A2M的斜率分别为k1 , k2 , 求k1k2的值.
【答案】解:(Ⅰ)依题意,F1(﹣1,0),F2(1,0),
设P(x,y),动圆P的比较为r,则|PF1|=1+r,|PF2|=5﹣r,
∴|PF1|+|PF2|=6,
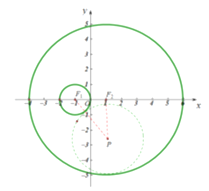
∴动圆圆心P的轨迹是以F1(﹣1,0)、F2(1,0)为焦点,长轴长为6的椭圆,
则b2=a2﹣c2=9﹣1=8,
于是曲线C的方程为:![]() +
+![]() =1;
=1;
(Ⅱ)由(I)可知A1(﹣3,0),A2(3,0),
设M(x,y),则![]() +
+![]() =1,
=1,
于是k1k2=![]()
![]() =
=![]() =
=![]() =﹣
=﹣![]() ;
;
【解析】(Ⅰ)通过设P(x,y)、动圆P的比较为r,利用圆与圆的位置关系可知|PF1|=1+r、|PF2|=5﹣r,进而化简可知动圆圆心P的轨迹是以F1(﹣1,0)、F2(1,0)为焦点、长轴长为6的椭圆,计算即得结论;
(Ⅱ)通过(I)可知A1(﹣3,0)、A2(3,0),通过设M(x,y),利用![]() +
+![]() =1及k1k2=
=1及k1k2=![]()
![]() 化简计算即得结论.
化简计算即得结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的数据作了初步处理,得到下面的散点图及一些统计量的值.
y(微克)
 x(千克)
x(千克)
|
|
|
|
|
|
|
3 | 38 | 11 | 10 | 374 | -121 | -751 |
其中![]()
(I)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为蔬菜农药残量
,哪一个适宜作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)若用解析式![]()
![]() 与用水量
与用水量![]() 的回归方程,求出
的回归方程,求出![]() 与
与![]() 的回归方程.(c,d精确到0.1)
的回归方程.(c,d精确到0.1)
(Ⅲ)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时对人体无害,为了放心食用该蔬菜,请估计需要用多少千克的清水清洗一千克蔬菜?(精确到0.1,参考数据![]() )
)
附:参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:


