题目内容
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() 平面
平面![]() .
.
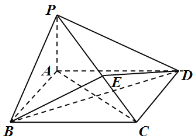
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的正切值.
的正切值.
【答案】(1)见解析 ; (2)3 .
【解析】
试题分析: (1)证明线面垂直,一般利用线面垂直判定及性质定理,经多次转化得证:先由线面垂直PA⊥平面ABCD得线线垂直PA⊥BD.同理PC⊥BD.,再由线线垂直得线面垂直BD⊥平面PAC. (2)求二面角正切值,一般利用空间直角坐标系,根据空间向量数量积进行求解:先建立恰当直角坐标系,设各点坐标,利用方程组得两平面法向量,再根据向量数量积求其夹角余弦值,最后根据同角三角函数关系求正切值.
试题解析:(1)证明 ∵PA⊥平面ABCD,BD平面ABCD,
∴PA⊥BD.
同理由PC⊥平面BDE,可证得PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC.
(2)解
如图,

分别以射线AB,AD,AP为x轴、y轴、z轴的正半轴建立空间直角坐标系.
由(1)知BD⊥平面PAC,
又AC平面PAC,∴BD⊥AC.
故矩形ABCD为正方形,
∴AB=BC=CD=AD=2.
∴A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,1).
∴![]() =(2,0,-1),
=(2,0,-1),![]() =(0,2,0),
=(0,2,0),![]() =(-2,2,0).
=(-2,2,0).
设平面PBC的一个法向量为n=(x,y,z),则
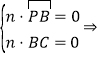
![]()
∴取x=1得n=(1,0,2).
∵BD⊥平面PAC,
∴![]() =(-2,2,0)为平面PAC的一个法向量.
=(-2,2,0)为平面PAC的一个法向量.
cos<n,![]() >=
>=![]()
设二面角B-PC-A的平面角为α,由图知0<α<![]() ,
,
∴cos α=![]() ,sin α=
,sin α=![]()
∴tan α=![]() =3,即二面角B-PC-A的正切值为3.
=3,即二面角B-PC-A的正切值为3.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目




