题目内容
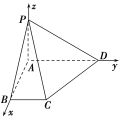
【题目】如图，在四棱锥PABCD中，PA⊥平面ABCD，PB与底面所成的角为45°，底面ABCD为直角梯形，∠ABC＝∠BAD＝90°，PA＝BC＝
AD＝1.问：在棱PD上是否存在一点E，使得CE∥平面PAB？若存在，求出E点的位置；若不存在，请说明理由．
【答案】见解析
【解析】
分别以AB，AD，AP所在直线为x，y，z轴建立空间直角坐标系，设E(0，y，z)，易知
＝(0,2,0)是平面PAB的法向量，利用
，确定出E点的位置.
分别以AB，AD，AP所在直线为x，y，z轴建立空间直角坐标系，如图，则P(0,0,1)，C(1,1,0)，D(0,2,0)，设E(0，y，z)，则
＝(0，y，z－1)，
＝(0,2，－1)．
∵∥，∴y(－1)－2(z－1)＝0.①
∵＝(0,2,0)是平面PAB的法向量，
＝(－1，y－1，z)，
∴由CE∥平面PAB，可得⊥.
∴(－1，y－1，z)·(0,2,0)＝2(y－1)＝0.
∴y＝1，代入①式得z＝
.
∴E是PD的中点，
即存在点E为PD中点时，CE∥平面PAB．
练习册系列答案
相关题目
