题目内容
19.“0<a<2”是“双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的离心率大于2”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 先写出双曲线的离心率e=$\sqrt{1+\frac{9}{{a}^{2}}}$,然后判断0<a<2能否得到e>2,e>2又能否得到0<a<2,这样根据充分条件、必要条件,以及必要不充分条件的概念即可找出正确选项.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{9}=1$的离心率e=$\frac{\sqrt{{a}^{2}+9}}{a}=\sqrt{1+\frac{9}{{a}^{2}}}$;
(1)若0<a<2,则0$<{a}^{2}<4,\frac{1}{{a}^{2}}>\frac{1}{4}$;
∴$1+\frac{9}{{a}^{2}}>\frac{13}{4}$;
∴$\sqrt{1+\frac{9}{{a}^{2}}}>\frac{\sqrt{13}}{2}$,即e>$\frac{\sqrt{13}}{2}$;
∵$\frac{\sqrt{13}}{2}<2$;
∴$e>\frac{\sqrt{13}}{2}$得不到e>2;
∴“0<a<2”不是“双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的离心率大于2”的充分条件;
(2)若双曲线的离心率大于2;
即$\sqrt{1+\frac{9}{{a}^{2}}}>2$,a>0;
∴解得$0<a<\sqrt{3}$;
∴一定得到0<a<2;
∴“0<a<2”是“双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的离心率大于2”的必要条件;
综上得“0<a<2”是“双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的离心率大于2”的必要不充分条件.
故选B.
点评 考查充分条件,必要条件,以及必要不充分条件的概念,双曲线离心率的概念及计算公式,不等式的性质.

| A. | (2,-2) | B. | (4,-3) | C. | (3,10) | D. | (-2,5) |
| A. | $\frac{80}{3}$ | B. | $\frac{255}{4}$ | C. | $\frac{624}{5}$ | D. | $\frac{1295}{6}$ |
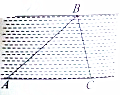 如图,在河岸边有一点A,河对岸有一点B,要测量A,B两点的距离,现在岸边取基线AC,测得AC=120m,∠BAC=45°,∠BCA=75°,求A,B两点间的距离.
如图,在河岸边有一点A,河对岸有一点B,要测量A,B两点的距离,现在岸边取基线AC,测得AC=120m,∠BAC=45°,∠BCA=75°,求A,B两点间的距离.