题目内容
4．
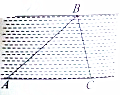如图，在河岸边有一点A，河对岸有一点B，要测量A，B两点的距离，现在岸边取基线AC，测得AC=120m，∠BAC=45°，∠BCA=75°，求A，B两点间的距离．
分析 根据三角形内角和定理，算出∠ABC=180°-75°-45°=60°，再由正弦定理，即可得出A、B两点的距离．
解答 解：∵在△ABC中，∠BAC=45°，∠BCA=75°，
∴∠ABC=180°-75°-45°=60°．
根据正弦定理，得$\frac{120}{sin60°}=\frac{AB}{sin75°}$，
∴AB=60$\sqrt{2}$+20$\sqrt{6}$（m）．
点评 本题给出实际应用问题，求河岸两边的A、B两点间的距离．着重考查了三角形内角和定理、正弦定理及其应用等知识，属于中档题．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
如图，四边形ABCD为矩形，AD⊥平面ABE，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE，
19．“0＜a＜2”是“双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1（a＞0）的离心率大于2”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
已知：过抛物线x2=4y的焦点F的直线交抛物线于A，B两个不同的点，过A，B分别作抛物线的切线，且二者相交于点C．