题目内容
已知函数f(x)=logax(a>0且a≠1),(x∈(0,+∞)),若x1,x2∈(0,+∞),判断 [f(x1)+f(x2)]与f(
[f(x1)+f(x2)]与f(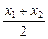 )的大小,并加以证明.
)的大小,并加以证明.
 [f(x1)+f(x2)]与f(
[f(x1)+f(x2)]与f(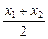 )的大小,并加以证明.
)的大小,并加以证明.  [f(x1)+f(x2)]≥f(
[f(x1)+f(x2)]≥f(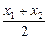 )(当且仅当x1=x2时取“=”号).
)(当且仅当x1=x2时取“=”号).f(x1)+f(x2)=logax1+logax2=logax1x2,
∵x1,x2∈(0,+∞),x1x2≤(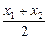 )2(当且仅当x1=x2时取“=”号),
)2(当且仅当x1=x2时取“=”号),
当a>1时,有logax1x2≤loga(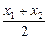 )2,
)2,
∴ logax1x2≤loga(
logax1x2≤loga(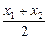 ),
), (logax1+logax2)≤loga
(logax1+logax2)≤loga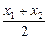 ,
,
即
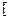 f(x1)+f(x2)]≤f(
f(x1)+f(x2)]≤f(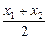 )(当且仅当x1=x2时取“=”号)
)(当且仅当x1=x2时取“=”号)
当0<a<1时,有logax1x2≥loga(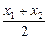 )2,
)2,
∴ (logax1+logax2)≥loga
(logax1+logax2)≥loga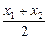 ,即
,即 [f(x1)+f(x2)]≥f(
[f(x1)+f(x2)]≥f(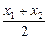 )(当且仅当x1=x2时取“=”号).
)(当且仅当x1=x2时取“=”号).
∵x1,x2∈(0,+∞),x1x2≤(
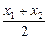 )2(当且仅当x1=x2时取“=”号),
)2(当且仅当x1=x2时取“=”号),当a>1时,有logax1x2≤loga(
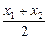 )2,
)2,∴
 logax1x2≤loga(
logax1x2≤loga(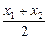 ),
), (logax1+logax2)≤loga
(logax1+logax2)≤loga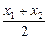 ,
,即

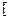 f(x1)+f(x2)]≤f(
f(x1)+f(x2)]≤f(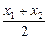 )(当且仅当x1=x2时取“=”号)
)(当且仅当x1=x2时取“=”号)当0<a<1时,有logax1x2≥loga(
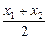 )2,
)2,∴
 (logax1+logax2)≥loga
(logax1+logax2)≥loga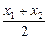 ,即
,即 [f(x1)+f(x2)]≥f(
[f(x1)+f(x2)]≥f(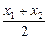 )(当且仅当x1=x2时取“=”号).
)(当且仅当x1=x2时取“=”号).
练习册系列答案
相关题目
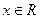 ,恒有
,恒有 成立,设向量a=
成立,设向量a=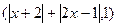 ,b=(1,2)。
,b=(1,2)。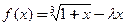 ,其中
,其中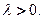
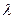 的取值范围,使得函数
的取值范围,使得函数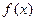 在
在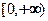 上是单调递减函数;
上是单调递减函数;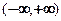 上?
上?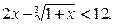
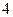 月份,有一新款服装投入某商场销售,
月份,有一新款服装投入某商场销售,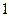 日该款服装仅销售出
日该款服装仅销售出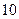 件,第二天售出
件,第二天售出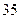 件,第三天销售
件,第三天销售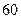 件,然后,每天售出的件数分别递增
件,然后,每天售出的件数分别递增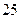 件,直到日销售量达到最大后,每天销售的件数分别递减
件,直到日销售量达到最大后,每天销售的件数分别递减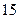 件,到月底该服装共销售出
件,到月底该服装共销售出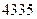 件.(Ⅰ)问
件.(Ⅰ)问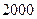 件时,社会上就流行,而日销售量连续下降,并低于
件时,社会上就流行,而日销售量连续下降,并低于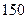 件时,则流行消失,问该款服装在社会上流行是否超过
件时,则流行消失,问该款服装在社会上流行是否超过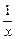 (x≤-
(x≤-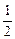 )的值域是( )
)的值域是( )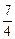
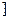
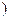
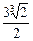 ,+∞
,+∞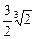 ]
]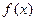 是定义域为[-3,3]的函数,并且设
是定义域为[-3,3]的函数,并且设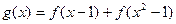 ,
,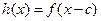 ,其中常数c为实数.(1)求
,其中常数c为实数.(1)求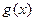 和
和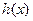 的定义域;(2)如果
的定义域;(2)如果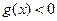 的自变量
的自变量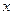 的取值范围.
的取值范围.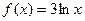 ;②
;②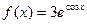 ;③
;③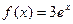 ;④
;④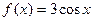 .其中对于
.其中对于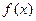 定义域内的任意一个自变量
定义域内的任意一个自变量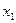 都存在唯一个自变量
都存在唯一个自变量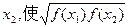 =3成立的函数是( ).
=3成立的函数是( ).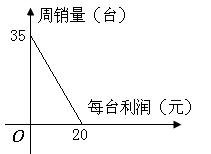
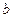 的原象可能不只一个;
的原象可能不只一个;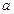 的象可能不只一个
的象可能不只一个