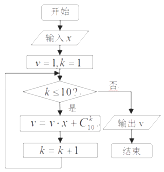
题目内容
【题目】在直角坐标系xOy中，直线l过点M（3，4），其倾斜角为45°，圆C的参数方程为 
．再以原点为极点，以x正半轴为极轴建立极坐标系，并使得它与直角坐标系xoy有相同的长度单位．
（1）求圆C的极坐标方程；
（2）设圆C与直线l交于点A、B，求|MA||MB|的值．
【答案】
（1）解：消去参数可得圆的直角坐标方程式为x2+（y﹣2）2=4，
由极坐标与直角坐标互化公式得（ρcosθ）2+（ρsinθ﹣2）2=4化简得ρ=4sinθ
（2）解：直线l的参数方程 
，（t为参数）．
即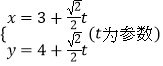 
代入圆方程得： 
+9=0，
设A、B对应的参数分别为t1、t2，则 
，t1t2=9，
于是|MA||MB|=|t1||t2|=|t1t2|=9
【解析】（1）利用cos2θ+sin2θ=1消去参数可得圆的直角坐标方程式，由极坐标与直角坐标互化公式代入化简即可得出．（2）直线l的参数方程 ，（t为参数），代入圆方程得： +9=0，利用|MA||MB|=|t1||t2|=|t1t2|即可得出．
习题精选系列答案
【题目】某同学在研究学习中，收集到某制药厂今年5个月甲胶囊生产产量（单位：万盒）的数据如下表所示：
| 1 | 2 | 3 | 4 | 5 |
| 5 | 5 | 6 | 6 | 8 |
若
线性相关，线性回归方程为
，则以下为真命题的是（ ）
A. 
每增加1个单位长度，则
一定增加0.7个单位长度
B. 每增加1个单位长度，则必减少0.7个单位长度
C. 当
时，的预测值为8.1万盒
D. 线性回归直线经过点
【题目】从一批苹果中，随机抽取50个，其重量（单位：克）的频数分布表如下：
分组（重量） |
|
|
|
|
频数（个） | 5 | 10 | 20 | 15 |
(1) 根据频数分布表计算苹果的重量在
的频率；
(2) 用分层抽样的方法从重量在
和
的苹果中共抽取4个，其中重量在
的有几个？
(3) 在（2）中抽出的4个苹果中，任取2个，求重量在
和
中各有1个的概率．
