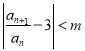题目内容
【题目】已知数列{an}是各项均为正整数的等差数列,公差d∈N* , 且{an}中任意两项之和也是该数列中的一项.
(1)若a1=4,则d的取值集合为;
(2)若a1=2m(m∈N*),则d的所有可能取值的和为 .
【答案】
(1){1,2,4}
(2)2m+1﹣1
【解析】解:由题意可得,ap+aq=ak , 其中p、q、k∈N* , 由等差数列的通向公式可得a1+(p﹣1)d+a1+(q﹣1)d=a1+(k﹣1),
整理得d= ![]() ,
,
1)若a1=4,则d= ![]() ,
,
∵p、q、k∈N* , 公差d∈N* ,
∴k﹣p﹣q+1∈N* ,
∴d=1,2,4,
故d的取值集合为 {1,2,4};
2)若a1=2m(m∈N*),则d= ![]() ,
,
∵p、q、k∈N* , 公差d∈N* ,
∴k﹣p﹣q+1∈N* ,
∴d=1,2,4,…,2m ,
∴d的所有可能取值的和为1+2+4+…+2m= ![]() =2m+1﹣1,
=2m+1﹣1,
所以答案是(1){1,2,4},(2)2m+1﹣1.
【考点精析】利用等比数列的前n项和公式和等差数列的性质对题目进行判断即可得到答案,需要熟知前![]() 项和公式:
项和公式: ;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.
;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案【题目】某校高三年级共有学生![]() 名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为
名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为![]() 分)进行统计,绘制出如下尚未完成的频率分布表:
分)进行统计,绘制出如下尚未完成的频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
(1)补充完整题中的频率分布表;
(2)若成绩在![]() 为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
【题目】下表是一个容量为20的样本数据分组后的频率分布表:
分组 |
|
|
|
| ||
频数 | 4 | 2 | 6 | 8 | ||
(1)请估计样本的平均数;
(2)以频率估计概率,若样本的容量为2000,求在分组![]() 中的频数;
中的频数;
(3)若从数据在分组![]() 与分组
与分组![]() 的样本中随机抽取2个,求恰有1个样本落在分组
的样本中随机抽取2个,求恰有1个样本落在分组![]() 的概率.
的概率.