题目内容
16.设函数f(x)=ex(2x-1)-ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是( )| A. | [$-\frac{3}{2e},1$) | B. | [$-\frac{3}{2e},\frac{3}{4}$) | C. | [$\frac{3}{2e},\frac{3}{4}$) | D. | [$\frac{3}{2e},1$) |
分析 设g(x)=ex(2x-1),y=ax-a,问题转化为存在唯一的整数x0使得g(x0)在直线y=ax-a的下方,求导数可得函数的极值,数形结合可得-a>g(0)=-1且g(-1)=-3e-1≥-a-a,解关于a的不等式组可得.
解答 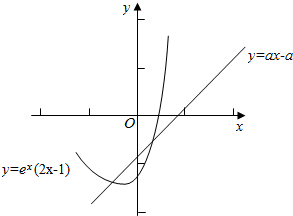 解:设g(x)=ex(2x-1),y=ax-a,
解:设g(x)=ex(2x-1),y=ax-a,
由题意知存在唯一的整数x0使得g(x0)在直线y=ax-a的下方,
∵g′(x)=ex(2x-1)+2ex=ex(2x+1),
∴当x<-$\frac{1}{2}$时,g′(x)<0,当x>-$\frac{1}{2}$时,g′(x)>0,
∴当x=-$\frac{1}{2}$时,g(x)取最小值-2${e}^{-\frac{1}{2}}$,
当x=0时,g(0)=-1,当x=1时,g(1)=e>0,
直线y=ax-a恒过定点(1,0)且斜率为a,
故-a>g(0)=-1且g(-1)=-3e-1≥-a-a,解得$\frac{3}{2e}$≤a<1
故选:D
点评 本题考查导数和极值,涉及数形结合和转化的思想,属中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
1.设x∈R,定义符号函数sgnx=$\left\{\begin{array}{l}{1,x>0}\\{0,x=0}\\{-1,x<0}\end{array}\right.$,则( )
| A. | |x|=x|sgnx| | B. | |x|=xsgn|x| | C. | |x|=|x|sgnx | D. | |x|=xsgnx |
8.已知函数f(x)=$\left\{\begin{array}{l}{2-|x|,x≤2}\\{(x-2)^{2},x>2}\end{array}\right.$,函数g(x)=b-f(2-x),其中b∈R,若函数y=f(x)-g(x)恰有4个零点,则b的取值范围是( )
| A. | ($\frac{7}{4}$,+∞) | B. | (-∞,$\frac{7}{4}$) | C. | (0,$\frac{7}{4}$) | D. | ($\frac{7}{4}$,2) |
 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{2}}}{2}$,点P(0,1)在短轴CD上,且$\overrightarrow{PC}$•$\overrightarrow{PD}$=-1
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{2}}}{2}$,点P(0,1)在短轴CD上,且$\overrightarrow{PC}$•$\overrightarrow{PD}$=-1