题目内容
4.已知函数f(x)=ax(x+r)2(a>0,r>0)(1)求f(x)的定义域,并讨论f(x)的单调性;
(2)若ar=400,求f(x)在(0,+∞)内的极值.
分析 (1)通过令分母不为0即得f(x)的定义域,通过求导即得f(x)的单调区间;
(2)通过(1)知x=r是f(x)的极大值点,计算即可.
解答 解:(1)∵函数f(x)=ax(x+r)2(a>0,r>0),
∴x≠-r,即f(x)的定义域为(-∞,-r)∪(-r,+∞).
又∵f(x)=ax(x+r)2=axx2+2rx+r2,
∴f′(x)=a(x2+2rx+r2)−ax(2x+2r)(x2+2rx+r2)2=a(r−x)(x+r)(x+r)4,
∴当x<-r或x>r时,f′(x)<0;当-r<x<r时,f′(x)>0;
因此,f(x)的单调递减区间为:(-∞,-r)、(r,+∞),递增区间为:(-r,r);
(2)由(1)的解答可得f′(x)=0,f(x)在(0,r)上单调递增,在(r,+∞)上单调递减,
∴x=r是f(x)的极大值点,
∴f(x)在(0,+∞)内的极大值为f(r)=ar(2r)2=a4r=4004=100.
点评 本题考查函数的定义域、单调区间、极值,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
19.根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )


| A. | 逐年比较,2008年减少二氧化硫排放量的效果最显著 | |
| B. | 2007年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
9.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
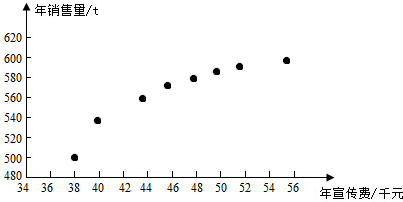
表中wi=√xi,¯w=18∑8i=1wi
(Ⅰ)根据散点图判断,y=a+bx与y=c+d√x哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1 v1),(u2 v2)…..(un vn),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:\widehat{β}=\frac{\sum_{i=1}^{n}({u}_{1}-\overline{u})({v}_{1}-\overline{v})}{\sum_{i=1}^{n}({u}_{1}-\overline{u})^{2}},\widehat{α}=\overline{v}-\widehat{β}\overline{u}.

| ¯x | ¯y | ¯w | ∑8i=1(xi-¯x)2 | ∑8i=1(wi-¯w)2 | ∑8i=1(xi-¯x)(yi-¯y) | ∑8i=1(wi-¯w)(yi-¯y) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
(Ⅰ)根据散点图判断,y=a+bx与y=c+d√x哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1 v1),(u2 v2)…..(un vn),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:\widehat{β}=\frac{\sum_{i=1}^{n}({u}_{1}-\overline{u})({v}_{1}-\overline{v})}{\sum_{i=1}^{n}({u}_{1}-\overline{u})^{2}},\widehat{α}=\overline{v}-\widehat{β}\overline{u}.
16.设函数f(x)=ex(2x-1)-ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是( )
| A. | [-\frac{3}{2e},1) | B. | [-\frac{3}{2e},\frac{3}{4}) | C. | [\frac{3}{2e},\frac{3}{4}) | D. | [\frac{3}{2e},1) |
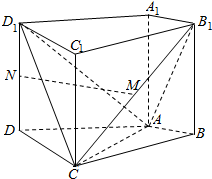 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD= 如题图,椭圆
如题图,椭圆