题目内容
6.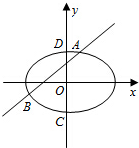 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{2}}}{2}$,点P(0,1)在短轴CD上,且$\overrightarrow{PC}$•$\overrightarrow{PD}$=-1
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{2}}}{2}$,点P(0,1)在短轴CD上,且$\overrightarrow{PC}$•$\overrightarrow{PD}$=-1(Ⅰ)求椭圆E的方程;
(Ⅱ)设O为坐标原点,过点P的动直线与椭圆交于A、B两点.是否存在常数λ,使得$\overrightarrow{OA}$•$\overrightarrow{OB}$+λ$\overrightarrow{PA}$•$\overrightarrow{PB}$为定值?若存在,求λ的值;若不存在,请说明理由.
分析 (Ⅰ)通过e=$\frac{{\sqrt{2}}}{2}$、$\overrightarrow{PC}$•$\overrightarrow{PD}$=-1,计算即得a=2、b=$\sqrt{2}$,进而可得结论;
(Ⅱ)分情况对直线AB斜率的存在性进行讨论:①当直线AB的斜率存在时,联立直线AB与椭圆方程,利用韦达定理计算可得当λ=1时$\overrightarrow{OA}$•$\overrightarrow{OB}$+λ$\overrightarrow{PA}$•$\overrightarrow{PB}$=-3;②当直线AB的斜率不存在时,$\overrightarrow{OA}$•$\overrightarrow{OB}$+λ$\overrightarrow{PA}$•$\overrightarrow{PB}$=-3.
解答 解:(Ⅰ)根据题意,可得C(0,-b),D(0,b),
又∵P(0,1),且$\overrightarrow{PC}$•$\overrightarrow{PD}$=-1,
∴$\left\{\begin{array}{l}{1-{b}^{2}=-1}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}-{b}^{2}={c}^{2}}\end{array}\right.$,解得a=2,b=$\sqrt{2}$,
∴椭圆E的方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1;
(Ⅱ)结论:存在常数λ=1,使得$\overrightarrow{OA}$•$\overrightarrow{OB}$+λ$\overrightarrow{PA}$•$\overrightarrow{PB}$为定值-3.
理由如下:
对直线AB斜率的存在性进行讨论:
①当直线AB的斜率存在时,设直线AB的方程为y=kx+1,
A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\\{y=kx+1}\end{array}\right.$,消去y并整理得:(1+2k2)x2+4kx-2=0,
∵△=(4k)2+8(1+2k2)>0,
∴x1+x2=-$\frac{4k}{1+2{k}^{2}}$,x1x2=-$\frac{2}{1+2{k}^{2}}$,
从而$\overrightarrow{OA}$•$\overrightarrow{OB}$+λ$\overrightarrow{PA}$•$\overrightarrow{PB}$=x1x2+y1y2+λ[x1x2+(y1-1)(y2-1)]
=(1+λ)(1+k2)x1x2+k(x1+x2)+1
=$\frac{(-2λ-4){k}^{2}+(-2λ-1)}{1+2{k}^{2}}$
=-$\frac{λ-1}{1+2{k}^{2}}$-λ-2.
∴当λ=1时,-$\frac{λ-1}{1+2{k}^{2}}$-λ-2=-3,
此时$\overrightarrow{OA}$•$\overrightarrow{OB}$+λ$\overrightarrow{PA}$•$\overrightarrow{PB}$=-3为定值;
②当直线AB的斜率不存在时,直线AB即为直线CD,
此时$\overrightarrow{OA}$•$\overrightarrow{OB}$+λ$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\overrightarrow{OC}•\overrightarrow{OD}$+$\overrightarrow{PC}•\overrightarrow{PD}$=-2-1=-3;
故存在常数λ=1,使得$\overrightarrow{OA}$•$\overrightarrow{OB}$+λ$\overrightarrow{PA}$•$\overrightarrow{PB}$为定值-3.
点评 本题考查椭圆的标准方程、直线方程等基础知识,考查推理论证能力、运算求解能力,考查数形结合、化归与转化、特殊与一般、分类与整合等数学思想,注意解题方法的积累,属于难题.

| A. | [$-\frac{3}{2e},1$) | B. | [$-\frac{3}{2e},\frac{3}{4}$) | C. | [$\frac{3}{2e},\frac{3}{4}$) | D. | [$\frac{3}{2e},1$) |
| A. | [-3,1] | B. | (-3,1) | C. | (-∞,-3]∪[1,+∞) | D. | (-∞,-3)∪(1,+∞) |
| 组号 | 分组 | 频数 |
| 1 | [4,5) | 2 |
| 2 | [5,6) | 8 |
| 3 | [6,7) | 7 |
| 4 | [7,8] | 3 |
(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
| A. | {3} | B. | {2,5} | C. | {1,4,6} | D. | {2,3,5} |
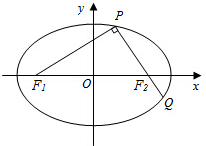 如题图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,且过F2的直线交椭圆于P,Q两点,且PQ⊥PF1.
如题图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,且过F2的直线交椭圆于P,Q两点,且PQ⊥PF1.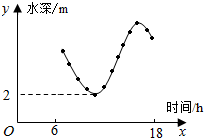 如图,某港口一天6时到18时的水渠变化曲线近似满足函数y=3sin($\frac{π}{6}$x+φ)+k.据此函数可知,这段时间水深(单位:m)的最大值为8.
如图,某港口一天6时到18时的水渠变化曲线近似满足函数y=3sin($\frac{π}{6}$x+φ)+k.据此函数可知,这段时间水深(单位:m)的最大值为8.