题目内容
5.若方程x2+ax+2b=0的一个根在(0,1)内,另一个根在(1,2)内,则$\frac{b-2}{a-1}$的取值范围是($\frac{1}{4}$,1).分析 设f(x)=x2+ax+2b,根据二次函数的性质与零点存在性定理可得f(0)>0、f(1)<0且f(2)>0.由此建立关于a、b的二元一次不等式组,设点E(a,b)为区域内的任意一点,根据直线的斜率公式可得k=$\frac{b-2}{a-1}$表示D、E连线的斜率,将点E在区域内运动并观察直线的倾斜角的变化,即可算出k的取值范围.
解答 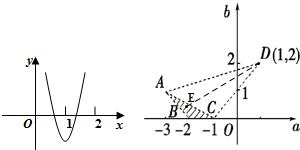 解:设f(x)=x2+ax+2b,
解:设f(x)=x2+ax+2b,
∵方程x2+ax+2b=0的一个根在区间(0,1)内,另一个根在区间(1,2)内,
∴可得 $\left\{\begin{array}{l}{f(0)=2b>0}\\{f(1)=1+a+2b<0}\\{f(2)=4+2a+2b>0}\end{array}\right.$.
作出满足上述不等式组对应的点(a,b)所在的平面区域,
得到△ABC及其内部,即如图所示的阴影部分(不含边界).
其中A(-3,1),B(-2,0),C(-1,0),
设点E(a,b)为区域内的任意一点,
则k=$\frac{b-2}{a-1}$,表示点E(a,b)与点D(1,2)连线的斜率.
∵KAD=$\frac{2-1}{1+3}$=$\frac{1}{4}$,kCD=$\frac{2-0}{1+1}$=1,结合图形可知:KAD<k<KCD,
∴k的取值范围是($\frac{1}{4}$,1),
故答案为:($\frac{1}{4}$,1).
点评 本题着重考查了二次函数的性质、零点存在性定理、二元一次不等式组表示的平面区域、直线的斜率公式与两点间的距离公式等知识,属于中档题.

练习册系列答案
相关题目
20.下列函数中,满足“f(x•y)=f(x)+f(y)”的单调递增函数是( )
| A. | f(x)=x2 | B. | f(x)=log2x | C. | f(x)=2x | D. | f(x)=log0.5x |
10. 某工厂于去年下半年对生产工艺进行了改造(每半年为一个生产周期),从去年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示,如图所示.已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润10元,生产一件合格品可获利润5元,生产一件次品要亏损5元
某工厂于去年下半年对生产工艺进行了改造(每半年为一个生产周期),从去年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示,如图所示.已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润10元,生产一件合格品可获利润5元,生产一件次品要亏损5元
(Ⅰ)试完成这个样本的50件产品的利润的频率分布表:
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
 某工厂于去年下半年对生产工艺进行了改造(每半年为一个生产周期),从去年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示,如图所示.已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润10元,生产一件合格品可获利润5元,生产一件次品要亏损5元
某工厂于去年下半年对生产工艺进行了改造(每半年为一个生产周期),从去年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示,如图所示.已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润10元,生产一件合格品可获利润5元,生产一件次品要亏损5元(Ⅰ)试完成这个样本的50件产品的利润的频率分布表:
| 利润(元) | 频数 | 频率 |
| 10 | 15 | 0.3 |
| 5 | 21 | 0.42 |
| -5 | 14 | 0.28 |
附:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
 如图,AD平分∠ABC,DE∥AC,EF∥BC,AB=15cm,AF=4cm,求BE和DE的长.
如图,AD平分∠ABC,DE∥AC,EF∥BC,AB=15cm,AF=4cm,求BE和DE的长.