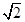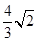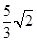题目内容
设x,y满足约束条件 ,
,
(1)画出不等式表示的平面区域,并求该平面区域的面积;
(2)若目标函数z=ax+by(a>0,b>0)的最大值为4,求 的最小值.
的最小值.
 ,
,(1)画出不等式表示的平面区域,并求该平面区域的面积;
(2)若目标函数z=ax+by(a>0,b>0)的最大值为4,求
 的最小值.
的最小值.(1)10;(2)4
试题分析:(1)如图

先在直角坐标系中画出各直线方程,再用特殊点代入法判断各不等式表示的平面区域,其公共部分即为不等式组表示的平面区域,用分割法即可求出其面积。(2)画出目标函数线,平移使其经过可行域当目标函数线的纵截距最大时,
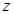 取得最大值,求出满足条件的此点坐标代入目标函数。用基本不等式求
取得最大值,求出满足条件的此点坐标代入目标函数。用基本不等式求 的最小值。
的最小值。试题解析:解:(1)不等式表示的平面区域如图所示阴影部分. 3分
联立
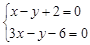 得点C坐标为(4,6)
得点C坐标为(4,6)平面区域的面积
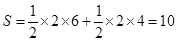 . 6分
. 6分(2)当直线ax+by=z(a>0,b>0)过直线x-y+2=0与直线3x-y-6=0的交点C(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大值4,即4a+6b=4,
即
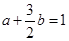 . 9分
. 9分所以
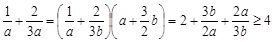
等号成立当且仅当
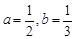 时取到.
时取到.故
 的最小值为4. 12分
的最小值为4. 12分
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 表示的平面区域内到直线y=2x-4的距离最远的点的坐标为________.
表示的平面区域内到直线y=2x-4的距离最远的点的坐标为________. 表示的平面区域的面积是________.
表示的平面区域的面积是________. 则2x-y+3的最小值是( )
则2x-y+3的最小值是( ) 则2x+3y的最小值是________.
则2x+3y的最小值是________. 则z=2x+4y的最小值为( ).
则z=2x+4y的最小值为( ). 位于曲线
位于曲线 与
与 所围成的封闭区域内,则
所围成的封闭区域内,则 的最小值为 .
的最小值为 .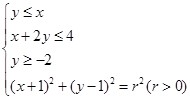 ,则r的最小值为( )
,则r的最小值为( )