题目内容
不等式组
表示的平面区域内到直线y＝2x－4的距离最远的点的坐标为________．
表示的平面区域内到直线y＝2x－4的距离最远的点的坐标为________．(－1,0)
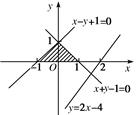
在坐标平面内画出不等式组表示的平面区域及直线y＝2x－4，结合图形可知，在该平面区域内所有的点中，点(－1,0)到直线y＝2x－4的距离最远．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
阳光课堂同步练习系列答案题目内容
表示的平面区域内到直线y＝2x－4的距离最远的点的坐标为________．阳光课堂同步练习系列答案
,
的最小值.
是由不等式组
所确定的平面区域内的动点，
是直线
上任意一点，
为坐标原点，则
的最小值为（ ）
及其内部,若目标函数
当且仅当在点
处取得最大值,则
的取值范围是______.
则z＝x－3y的最小值为________．
=(1,
),
=(0,1),O为坐标原点,动点P(x,y)满足0≤
·
满足
则
的最小值是（ ）