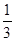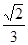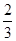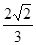题目内容
设抛物线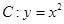 ,
,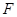 为焦点,
为焦点,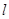 为准线,准线与
为准线,准线与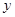 轴交点为
轴交点为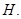
(1)求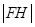 ;
;
(2)过点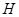 的直线与抛物线
的直线与抛物线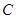 交于
交于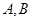 两点,直线
两点,直线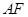 与抛物线交于点
与抛物线交于点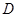 .
.
①设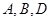 三点的横坐标分别为
三点的横坐标分别为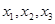 ,计算:
,计算: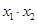 及
及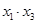 的值;
的值;
②若直线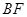 与抛物线交于点
与抛物线交于点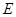 ,求证:
,求证: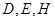 三点共线.
三点共线.
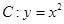 ,
,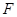 为焦点,
为焦点,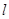 为准线,准线与
为准线,准线与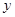 轴交点为
轴交点为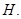
(1)求
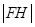 ;
;(2)过点
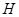 的直线与抛物线
的直线与抛物线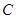 交于
交于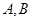 两点,直线
两点,直线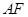 与抛物线交于点
与抛物线交于点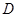 .
.①设
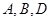 三点的横坐标分别为
三点的横坐标分别为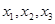 ,计算:
,计算: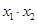 及
及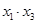 的值;
的值;②若直线
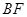 与抛物线交于点
与抛物线交于点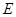 ,求证:
,求证: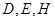 三点共线.
三点共线.(1) 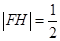 (2)
(2) 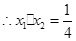 ,
,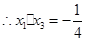 ,并根据斜率相等来证明三点共线。
,并根据斜率相等来证明三点共线。
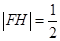 (2)
(2) 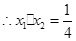 ,
,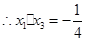 ,并根据斜率相等来证明三点共线。
,并根据斜率相等来证明三点共线。试题分析:(1)
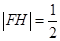
(2)设直线
 方程:
方程: ,直线
,直线 方程:
方程:


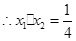


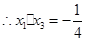
设



 三点共线。
三点共线。点评:解决的关键是利用抛物线的定义,以及联立方程组的思想来得到根与系数的关系,结合点的坐标来求解斜率,确定点的位置,属于基础题。

练习册系列答案
相关题目
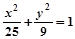 (y≠0)
(y≠0)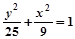 (y≠0)
(y≠0)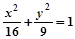 (y≠0)
(y≠0)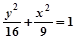 (y≠0)
(y≠0)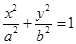 (a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )
(a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )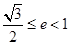
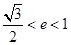
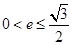

 倍
倍 倍
倍 倍
倍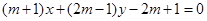 经过的定点的坐标是 .
经过的定点的坐标是 .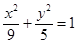 的中心为顶点,右焦点为焦点的抛物线方程是 .
的中心为顶点,右焦点为焦点的抛物线方程是 .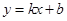 与曲线
与曲线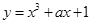 相切于点
相切于点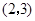 ,则
,则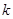 的值为 ( )
的值为 ( )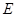 :
: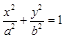 (
(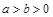 )过点
)过点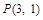 ,其左、右焦点分别为
,其左、右焦点分别为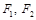 ,且
,且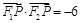 .
.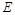 的方程;
的方程;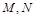 是直线
是直线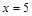 上的两个动点,且
上的两个动点,且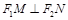 ,则以
,则以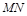 为直径的圆
为直径的圆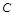 是否过定点?请说明理由.
是否过定点?请说明理由.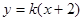
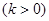 与抛物线
与抛物线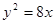 相交于
相交于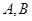 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若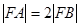 ,则k的值为( )。
,则k的值为( )。