题目内容

15．在△ABC中，角A，B所对的边分别为a，b，若a=3bsinA，则sinB=$\frac{1}{3}$．

分析 由条件利用正弦定理求得sinB的值．

解答 解：△ABC中，角A，B所对的边分别为a，b，若a=3bsinA，则由正弦定理可得sinA=3sinBsinA，
求得sinB=$\frac{1}{3}$，
故答案为：$\frac{1}{3}$．

点评 本题主要考查正弦定理的应用，属于基础题．

练习册系列答案
相关题目
5．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点分别为F1，F2，P为椭圆上一点，且∠F1PF2=120°，则椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率的取值范围为[$\frac{\sqrt{3}}{2}$，1）．
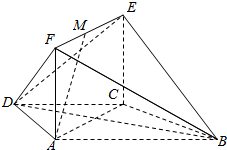6．如图，在等腰梯形ABCD中，AB∥CD，AD=DC=a，∠ABC=60°，平面ACEF⊥平面ABCD，四边形ACEF是平行四边形，点M在线段EF上．
（1）求证：BC⊥平面ACEF；
（2）当FM为何值时，AM∥平面BDE？证明你的结论．
3．（1）计算eln3+（0.01）${\;}^{-\frac{1}{2}}$+（1-$\sqrt{3}$）0
（2）若2lg（x-2y）=lgy+lg（5x-4y），求log2$\frac{x}{y}$的值．
10．已知等比数列{an}的前n项和为Sn，且5S1，2S2，S3成等差数列．
（1）求{an}的公比q；
（2）当a1-a3=3时，证明：数列{Sn-1}也是等比数列．
20．已知三角形ABC中，A为锐角，且$\sqrt{3}$b=2asinB
（1）求A，
（2）若a=7，三角形ABC的面积为10$\sqrt{3}$，求b+c的值．
7．已知△ABC的内角A，B，C所对的边分别为a，b，c，且满足bsin（A+B）-$\sqrt{3}$ccosB=0．
（1）求B；
（2）若b=$\sqrt{7}$，c=2，求△ABC的面积．
4．若a=3a+1，b=ln2，c=log2sin$\frac{π}{12}$，则（　　）
A．b＞a＞cB．a＞b＞cC．c＞a＞bD．b＞c＞a
5．判断下列函数是否为奇函数：
（1）f（x）=$\frac{1}{x}$+2；
（2）f（x）=x3+2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网