题目内容
13．若椭圆的长轴与短轴之比为2，它的右焦点是（2$\sqrt{15}$，0）求椭圆的标准方程．分析 由题意可得a=2b，c=2$\sqrt{15}$，由c2=a2-b2=60，解方程可得a，b，进而得到椭圆方程．
解答 解：椭圆的长轴与短轴之比为2，可得a=2b，
它的右焦点是（2$\sqrt{15}$，0），即c=2$\sqrt{15}$，
由c2=a2-b2=60，
解得a2=80，b2=20．
即有椭圆的标准方程为$\frac{{x}^{2}}{80}$+$\frac{{y}^{2}}{20}$=1．
点评 本题考查椭圆的方程和性质，考查椭圆的a，b，c的关系和运算能力，属于基础题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
3．已知函数f（x）=x2-（2m+6）x+m+4．
（Ⅰ）若对于任意m∈[-1，1]，f（x）＞0恒成立，求实数x的取值范围；
（Ⅱ）若对于任意x∈[-1，1]，f（x）≥0恒成立，求实数m的取值范围．
（Ⅰ）若对于任意m∈[-1，1]，f（x）＞0恒成立，求实数x的取值范围；
（Ⅱ）若对于任意x∈[-1，1]，f（x）≥0恒成立，求实数m的取值范围．
1．下列函数中，既是偶函数，又在区间（0，+∞）上单调递减的函数是（ ）
| A． | y=x2 | B． | y=x-1 | C． | $y={x^{-\frac{2}{3}}}$ | D． | y=x${\;}^{\frac{1}{3}}$ |
如图是正方体截去阴影部分所得的几何体，则该几何体的左视图是 （ ）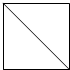
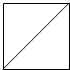
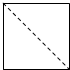
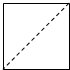
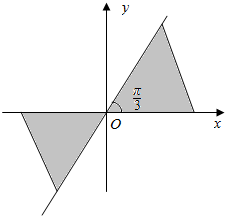如图所示，阴影部分表示的角的集合为（含边界）{α|kπ≤α≤kπ+$\frac{π}{3}$，k∈Z}（用弧度表示）．