题目内容
已知函数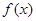 是定义在
是定义在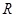 的奇函数,当
的奇函数,当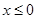 时,
时,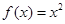 ,若对任意的
,若对任意的 ,不等式
,不等式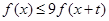 恒成立,则实数
恒成立,则实数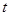 的最大值为( )
的最大值为( )
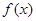 是定义在
是定义在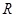 的奇函数,当
的奇函数,当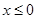 时,
时,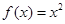 ,若对任意的
,若对任意的 ,不等式
,不等式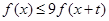 恒成立,则实数
恒成立,则实数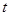 的最大值为( )
的最大值为( )A.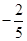 | B.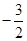 | C.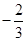 | D.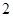 |
A
试题分析:当
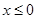 时,
时,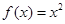 ,∵函数是奇函数∴当x>0时,
,∵函数是奇函数∴当x>0时,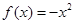 ,
,∴
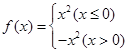 ∴f(x)在R上是单调递减函数,且满足9f(x+t)=f(3x+3t),
∴f(x)在R上是单调递减函数,且满足9f(x+t)=f(3x+3t),不等式f(x)≤9f(x+t)在[t,t+1]恒成立,x≥3x+3t在[t,t+1]恒成立,
即:
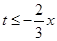 在[t,t+1]恒成立,
在[t,t+1]恒成立,∴
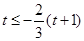 ,解得
,解得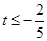 ,故实数t的最大值是
,故实数t的最大值是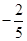 .
.故选:A.

练习册系列答案
相关题目
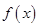 在
在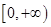 单调递减,
单调递减,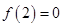 .若
.若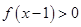 ,则
,则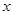 的取值范围是__________.
的取值范围是__________.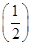 1-x,则:
1-x,则: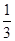 )的x的取值范围是( )
)的x的取值范围是( )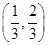
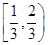
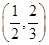
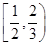
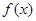 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当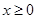 时,
时,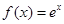 。若对任意的x
。若对任意的x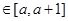 ,不等式
,不等式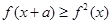 恒成立,则实数a的最大值是( )。
恒成立,则实数a的最大值是( )。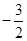
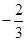
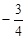
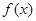 在
在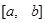 上的最大值和最小值分别为
上的最大值和最小值分别为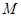 、
、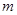 ,那么
,那么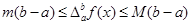 .根据这一结论求出
.根据这一结论求出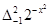 的取值范围( ).
的取值范围( ).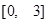
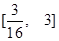

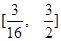
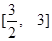
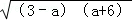 (﹣6≤a≤3)的最大值为( )
(﹣6≤a≤3)的最大值为( )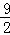
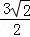
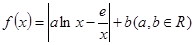 且
且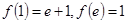 ,求函数
,求函数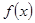 的单调区间.
的单调区间.