Question

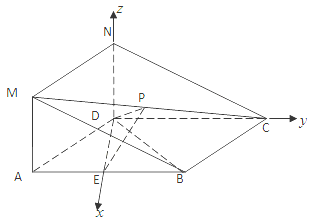
【题目】在如图所示的几何体中，四边形是菱形，是矩形，平面平面，，，，为的中点．

（1）求证：；

（2）在线段上是否存在点，使二面角的大小为，若存在，求出的值，若不存在，请说明理由．

Answer 1

【答案】（1） 见解析（2）

【解析】分析：(1)结合题中所给的条件，利用面面垂直的条件以及题中所给的特殊几何图形，得到相应的垂直关系，之后借助于线面垂直来得到线线垂直.

(2)对于存在性问题，可先假设存在，即假设线段上存在点，使二面角的大小为，再通过建立空间直角坐标系，求出相关点的坐标，结合向量的数量积求出二面角的大小，若出现矛盾，则说明假设不成立，即不存在，否则存在.

详解：（1）证明：连接，

∵，，∴△为等边三角形，

又∵为中点，∴，

又∵，∴，

∵为矩形，∴，

又∵平面平面，平面平面 ，平面，

∴平面，

又∵平面，∴，

又∵，，

∴平面，

∵平面，

∴．

（2）由（1）知平面，

∵、平面，

∴，，

又∵，以为坐标原点，、、分别为轴、轴、轴建立空间直角坐标系，则，，，，，

设，，，，

设平面的一个法向量为，，

则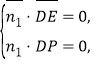即令，则，

由图形知，平面的一个法向量，

由题意知，

即，即，

∵，∴．