题目内容
【题目】在等腰直角三角形ABC中,AB=AC=4,点P是边AB边上异于AB的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的重心,则AP等于( )
A.2
B.1
C.![]()
D.![]()
【答案】D
【解析】解:建立如图所示的坐标系:
可得B(4,0),C(0,4),故直线BC的方程为x+y=4,
△ABC的重心为( ![]() ,
, ![]() ),设P(a,0),其中0<a<4,
),设P(a,0),其中0<a<4,
则点P关于直线BC的对称点P1(x,y),满足 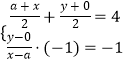 ,
,
解得 ![]() ,即P1(4,4﹣a),易得P关于y轴的对称点P2(﹣a,0),
,即P1(4,4﹣a),易得P关于y轴的对称点P2(﹣a,0),
由光的反射原理可知P1 , Q,R,P2四点共线,
直线QR的斜率为k= ![]() =
= ![]() ,故直线QR的方程为y=
,故直线QR的方程为y= ![]() (x+a),
(x+a),
由于直线QR过△ABC的重心( ![]() ,
, ![]() ),代入化简可得3a2﹣4a=0,
),代入化简可得3a2﹣4a=0,
解得a= ![]() ,或a=0(舍去),故P(
,或a=0(舍去),故P( ![]() ,0),故AP=
,0),故AP= ![]()
故选D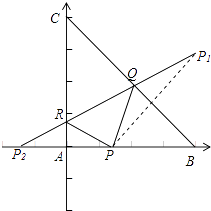

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】甲、乙两个篮球队在4次不同比赛中的得分情况如下:
甲队 | 88 | 91 | 92 | 96 |
乙队 | 89 | 93 | 9▓ | 92 |
乙队记录中有一个数字模糊(即表中阴影部分),无法确认,假设这个数字具有随机性,并用![]() 表示.
表示.
(Ⅰ)在4次比赛中,求乙队平均得分超过甲队平均得分的概率;
(Ⅱ)当![]() 时,分别从甲、乙两队的4次比赛中各随机选取1次,记这2个比赛得分之差的绝对值为
时,分别从甲、乙两队的4次比赛中各随机选取1次,记这2个比赛得分之差的绝对值为![]() ,求随机变量
,求随机变量![]() 的分布列;
的分布列;
(Ⅲ)如果乙队得分数据的方差不小于甲队得分数据的方差,写出![]() 的取值集合.(结论不要求证明)
的取值集合.(结论不要求证明)
