题目内容
4.已知f(x)是定义在R上的奇函数,x≥0时,f(x)=x2+$\sqrt{x+1}$+a,则f(-1)=$-\sqrt{2}$.分析 先利用奇函数的性质f(0)=0,计算a的值,再利用已知函数解析式,计算f(1)的值,最后利用奇函数的对称性求得f(-1).
解答 解:∵当x≥0时,$f(x)={x^2}+\sqrt{x+1}+a$,∴f(1)=1+$\sqrt{2}$+a
∵f(x)是定义在R上的奇函数
∴f(0)=1+a=0,∴a=-1
∴f(-1)=-f(1)=-$\sqrt{2}$.
故答案为:$-\sqrt{2}$.
点评 本题主要考查了奇函数的定义和性质运用,利用奇函数的性质求得a的值是解决本题的关键,属基础题

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
15.设f(x)是(x2+$\frac{1}{2x}$)6展开式的中间项,若存在x∈[$\frac{\sqrt{2}}{2}$,$\sqrt{2}$]使f(x)≤mx成立,则实数m的取值范围是( )
| A. | (-∞,$\frac{5}{4}$) | B. | (-∞,$\frac{5}{4}$] | C. | ($\frac{5}{4}$,+∞) | D. | [$\frac{5}{4}$,+∞) |
19.已知集合A={x|x2-2x-3<0},B={x|x2<9},则( )
| A. | A?B | B. | B?A | C. | A=B | D. | A∩B=Φ |
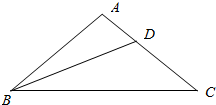 △ABC中,AD:DC=5:9,△ABD的面积为22.5cm2,那么△BDC的面积是多少?△ABC的面积是多少?
△ABC中,AD:DC=5:9,△ABD的面积为22.5cm2,那么△BDC的面积是多少?△ABC的面积是多少?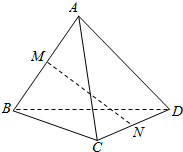 如图,空间四边形ABCD的每条边和AC,BD的长都等于a,点M,N分别是AB,CD的中点,求证:MN⊥AB,MN⊥CD.
如图,空间四边形ABCD的每条边和AC,BD的长都等于a,点M,N分别是AB,CD的中点,求证:MN⊥AB,MN⊥CD.