题目内容
若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1,则椭圆长轴的最小值为( )
| A.1 | B. | C.2 | D.2 |
D
解析试题分析:由题意知bc=1.∴a2=b2+c2=b2+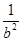 ≥2,∴a≥
≥2,∴a≥ .∴2a≥2
.∴2a≥2 ,故选D.
,故选D.
考点:本题主要考查椭圆的几何性质,均值定理的应用。
点评:简单题,思路明确,这要从给定a,b,c关系入手,确定a的表达式,应用均值定理得到其最小值。

练习册系列答案
相关题目
设 、
、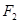 分别是椭圆
分别是椭圆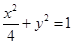 的左、右焦点,
的左、右焦点, 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且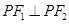 ,则点
,则点 的横坐标为
的横坐标为
A.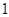 | B.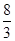 | C.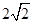 | D.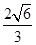 |
若抛物线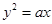 的焦点到准线的距离为4,则此抛物线的焦点坐标为
的焦点到准线的距离为4,则此抛物线的焦点坐标为
A.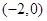 | B.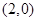 | C.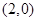 或 或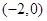 | D.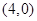 |
以抛物线 的焦点为圆心,且过坐标原点的圆的方程为( )
的焦点为圆心,且过坐标原点的圆的方程为( )
A. | B. |
C. | D. |
设双曲线 的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则|
的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则| |=
|=
A.5 | B.4 | C.3 | D.2 |


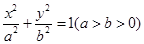 与双曲线
与双曲线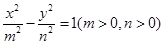 有相同的焦点
有相同的焦点 和
和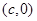 ,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为
,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为

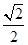
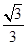
 的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).
的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).




 ,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )



