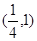题目内容
设圆 的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).
的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).
A. | B. |
C. | D. |
D
解析试题分析:∵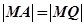 ,∴
,∴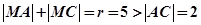 ,∴动点M的轨迹为以A、C为焦点的椭圆,∴
,∴动点M的轨迹为以A、C为焦点的椭圆,∴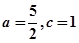 ,∴
,∴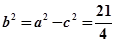 ,∴动点M的轨迹方程为
,∴动点M的轨迹方程为
考点:本题考查了轨迹方程的求法
点评:利用常见解析几何的定义转化求解动点轨迹问题是解决此类问题的关键,属基础题

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
椭圆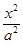 +
+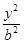 =1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=
=1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=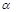 , 且
, 且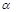 ∈[
∈[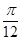 ,
,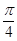 ], 则该椭圆离心率的取值范围为 ( )
], 则该椭圆离心率的取值范围为 ( )
A.[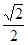 ,1 ) ,1 ) | B.[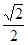 , ,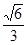 ] ] | C.[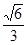 , 1) , 1) | D.[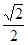 , ,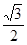 |
若抛物线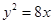 上一点
上一点 到其焦点的距离为
到其焦点的距离为 ,则点
,则点 的坐标为( )
的坐标为( )
A.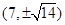 | B. | C. | D. |
若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1,则椭圆长轴的最小值为( )
| A.1 | B. | C.2 | D.2 |
在平面直角坐标系 中,双曲线中心在原点,焦点在
中,双曲线中心在原点,焦点在 轴上,一条渐近线方程为
轴上,一条渐近线方程为 ,
,
则它的离心率为( )
A. | B. | C. | D. |
若点 到双曲线
到双曲线
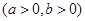 的一条渐近线的距离为
的一条渐近线的距离为 ,则该双曲线的离心率为
,则该双曲线的离心率为
A. | B. | C. | D. |
 等边三角形的圆锥,过底面圆周上任一点作一平面
等边三角形的圆锥,过底面圆周上任一点作一平面 ,且
,且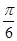 ,已知
,已知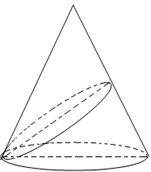
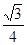



 右支上一点,F1、F2分别为双曲线的左、右焦点,I为
右支上一点,F1、F2分别为双曲线的左、右焦点,I为 的内心,若
的内心,若 成立,则
成立,则 的值为 ( )
的值为 ( )



 上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )