Question

【题目】已知椭圆：．

（1）若抛物线的焦点与的焦点重合，求的标准方程；

（2）若的上顶点、右焦点及轴上一点构成直角三角形，求点的坐标；

（3）若为的中心，为上一点(非的顶点)，过的左顶点，作，交轴于点，交于点，求证：．

Answer 1

【答案】（1）抛物线的标准方程为和．

（2）或．

（3）见解析

【解析】

（1）根据椭圆的方程和抛物线的性质即可求出；

（2）按哪个角为直角进行分类，结合数量积为0，计算得到M的坐标.

（3）由B（﹣3，0），BQ∥OP，设直线BQ的方程为x＝my﹣3，直线OP的方程为x＝my，分别于椭圆的方程联立，求出点Q，N，P的坐标，再根据向量的运算即可证明.

(1) 椭圆的焦点坐标为和，抛物线的标准方程为和．

(2)设点的坐标为，的上顶点的坐标为，右焦点的坐标为．

当为直角顶点时，点的坐标为；

当为直角顶点时，，，由，解得，点的坐标为．

因此，点的坐标为或．

(3)设直线的方程为()，直线的方程为．

于是点，的坐标，为方程组的实数解，

解得点的坐标为．

点，的坐标，为方程组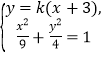的实数解，解得点的坐标为．

又点的坐标为．

于是，，，

，

，

即，得证．