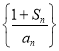Question

【题目】设数列的各项均为不等的正整数，其前项和为，我们称满足条件“对任意的，均有”的数列为“好”数列．

（1）试分别判断数列，是否为“好”数列，其中，，，并给出证明；

（2）已知数列为“好”数列．

① 若，求数列的通项公式；

② 若，且对任意给定正整数（），有成等比数列，求证：．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）由，运用等差数列的求和公式，通过检验即可判断（2）对任意的，均有，令，则，即，消去，可得从而证明为等差数列，①进而求其通项公式② 若，则，由成等比数列，运用等比中项性质，结合等差数列的通项公式，化简整理，求得的表达式，分析整理由不等式性质，即可得证.

（1）若，则，所以，

而，

所以对任意的均成立，

即数列是“好”数列；

若，取，

则，，

此时，

即数列不是“好”数列．

（2）因为数列为“好”数列，取，则，即恒成立．

当，有，

两式相减，得（），

即（），

所以（），

所以，

即，即（），

当时，有，即，

所以对任意，恒成立，

所以数列是等差数列．

设数列的公差为，

① 若，则，即，

因为数列的各项均为不等的正整数，所以，

所以，，所以．

② 若，则，

由成等比数列，得，所以，

即

化简得，，

即．

因为是任意给定正整数，要使，必须，

不妨设，由于是任意给定正整数，

所以．