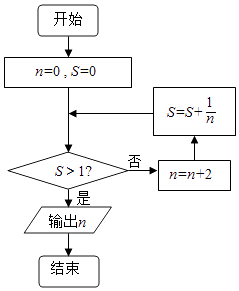
题目内容
【题目】集合M的若干个子集的集合称为集合M的一个子集族.对于集合{1,2,3…n}的一个子集族D满足如下条件:若A∈D,BA,则B∈D,则称子集族D是“向下封闭”的. (Ⅰ)写出一个含有集合{1,2}的“向下封闭”的子集族D并计算此时 ![]() 的值(其中|A|表示集合A中元素的个数,约定||=0;
的值(其中|A|表示集合A中元素的个数,约定||=0; ![]() 表示对子集族D中所有成员A求和);
表示对子集族D中所有成员A求和);
(Ⅱ)D是集合{1,2,3…n}的任一“向下封闭的”子集族,对A∈D,记k=max|A|, ![]() (其中max表示最大值),
(其中max表示最大值),
(ⅰ)求f(2);
(ⅱ)若k是偶数,求f(k).
【答案】解:(Ⅰ)含有集合{1,2}的“向下封闭”的子集族D={,{1},{2},{1,2}} 此时 ![]()
(Ⅱ)设{1,2,3…n}的所有不超过k个元素的子集族为Dk ,
(ⅰ)易知当D=D2时, ![]() 达到最大值,
达到最大值,
∴ ![]()
(ⅱ)设D是使得k=max|A|的任一个“向下封闭”的子集族,记D=D′∪D',其中D′为不超过k﹣2元的子集族,D'为k﹣1元或k元的子集,
则 ![]() =
= 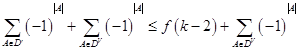
现设D'有l( ![]() )个{1,2,3…n}的k元子集,由于一个k﹣1元子集至多出
)个{1,2,3…n}的k元子集,由于一个k﹣1元子集至多出
现在n﹣k+1个{1,2,3…n}的k元子集中,而一个k元子集中有 ![]() 个k﹣1元子集,故l个k元子集至少产生
个k﹣1元子集,故l个k元子集至少产生 ![]() 个不同的k﹣1元子集.
个不同的k﹣1元子集. 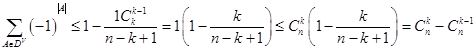
![]()
由(ⅰ)得 ![]()
【解析】(Ⅰ)求出含有集合{1,2}的“向下封闭”的子集族D,并计算此时 ![]() 的值;(Ⅱ)设{1,2,3…n}的所有不超过k个元素的子集族为Dk , (ⅰ)易知当D=D2时,
的值;(Ⅱ)设{1,2,3…n}的所有不超过k个元素的子集族为Dk , (ⅰ)易知当D=D2时, ![]() 达到最大值,求出f(2)的值即可;(ⅱ)设D是使得k=max|A|的任一个“向下封闭”的子集族,记D=D′∪D',其中D′为不超过k﹣2元的子集族,D'为k﹣1元或k元的子集,则求出
达到最大值,求出f(2)的值即可;(ⅱ)设D是使得k=max|A|的任一个“向下封闭”的子集族,记D=D′∪D',其中D′为不超过k﹣2元的子集族,D'为k﹣1元或k元的子集,则求出 ![]() ,设D'有l(
,设D'有l( ![]() )个{1,2,3…n}的k元子集,由于一个k﹣1元子集至多出现在n﹣k+1个{1,2,3…n}的k元子集中,而一个k元子集中有
)个{1,2,3…n}的k元子集,由于一个k﹣1元子集至多出现在n﹣k+1个{1,2,3…n}的k元子集中,而一个k元子集中有 ![]() 个k﹣1元子集,故l个k元子集至少产生
个k﹣1元子集,故l个k元子集至少产生 ![]() 个不同的k﹣1元子集,求出f(k)即可.
个不同的k﹣1元子集,求出f(k)即可.
【考点精析】掌握子集与真子集是解答本题的根本,需要知道任何一个集合是它本身的子集;n个元素的子集有2n个,n个元素的真子集有2n -1个,n个元素的非空真子集有2n-2个.

【题目】某校高三共有900名学生,高三模拟考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
组号 | 第一组 | 第二组 | 第二组 | 第四组 |
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 6 | 4 | 22 | 20 |
频率 | 0.06 | 0.04 | 0.22 | 0.20 |
组号 | 第五组 | 第六组 | 第七组 | 第八组 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 18 | a | 10 | 5 |
频率 | b | 0.15 | 0.10 | 0.05 |
(1)若频数的总和为c,试求a,b,c的值;
(2)为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生,在这6名学生中又再随机抽取2名与心理老师面谈,令第七组被抽中的学生数为随机变量ξ,求随机变量ξ的分布列和数学期望;
(3)估计该校本次考试的数学平均分.