题目内容
从空间一点P向二面角α-1-β的两个平面作垂线PE,PF,E,F为垂足,若∠EPF=60°,则二面角的平面角的大小为( )
| A、60° | B、120° |
| C、60°或120° | D、不确定 |
考点:二面角的平面角及求法
专题:空间向量及应用
分析:首先,确定∠EPF=60°就是两个平面α和β的法向量的夹角,然后,利用二面角的平面角和法向量的夹角直接的关系确定即可.
解答:
解:∠EPF=60°就是两个平面α和β的法向量的夹角,
它与二面角的平面角相等或互补,
故二面角的平面角的大小为60°或120°.
故选:C.
它与二面角的平面角相等或互补,
故二面角的平面角的大小为60°或120°.
故选:C.
点评:本题重点考查了平面的法向量、法向量的夹角与平面所成的二面角之间的关系等知识,属于中档题.

练习册系列答案
相关题目
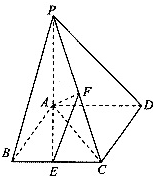 如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥面ABCD,AP=AB,E、F分别是BC、PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥面ABCD,AP=AB,E、F分别是BC、PC的中点.(1)求证:AE⊥平面PAD;
(2)求四棱锥A-BEFP的体积.
黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
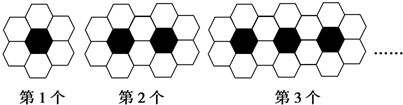
则第n个图案中的白色地面砖有( )

则第n个图案中的白色地面砖有( )
| A、4n-2块 |
| B、4n+2块 |
| C、3n+3块 |
| D、3n-3块 |