题目内容
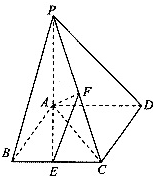 如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥面ABCD,AP=AB,E、F分别是BC、PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥面ABCD,AP=AB,E、F分别是BC、PC的中点.(1)求证:AE⊥平面PAD;
(2)求四棱锥A-BEFP的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)根据线面垂直的判定定理即可证明AE⊥平面PAD;
(2)根据棱锥的体积公式,利用割补法即可求四棱锥A-BEFP的体积.
(2)根据棱锥的体积公式,利用割补法即可求四棱锥A-BEFP的体积.
解答:
 证明:(1)依题意,在等腰△ABC中,∠ABC=60°,
证明:(1)依题意,在等腰△ABC中,∠ABC=60°,
∴△ABC为等边三角形,又E是BC的中点,
∴AE⊥BC,又BC∥AD,
∴AE⊥AD;
∵PA⊥底面ABCD,AE?底面ABCD,
∴AE⊥PA;
PA∩AD=A,
∴AE⊥平面PAD
(2)连结OF,则OF是△PAC的中位线,
则OF⊥平面ABCD,且OF=
AP=1,
则四棱锥A-BEFP的体积V四棱锥A-BEFP=VP-ABC-VF-AEC=
•S△ABC•PA-
S△AEC•OF
=
×
×22×
×2-
×
×
×22×
×1=
.
 证明:(1)依题意,在等腰△ABC中,∠ABC=60°,
证明:(1)依题意,在等腰△ABC中,∠ABC=60°,∴△ABC为等边三角形,又E是BC的中点,
∴AE⊥BC,又BC∥AD,
∴AE⊥AD;
∵PA⊥底面ABCD,AE?底面ABCD,
∴AE⊥PA;
PA∩AD=A,
∴AE⊥平面PAD
(2)连结OF,则OF是△PAC的中位线,
则OF⊥平面ABCD,且OF=
| 1 |
| 2 |
则四棱锥A-BEFP的体积V四棱锥A-BEFP=VP-ABC-VF-AEC=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查线面垂直的判定,以及棱锥的体积的计算,利用割补法是解决本题的关键.

练习册系列答案
相关题目
若tanα=lg(10a),tanβ=lg(
),且α+β=
,则实数a的值为( )
| 1 |
| a |
| π |
| 4 |
| A、1 | ||
B、
| ||
C、1或
| ||
| D、1或10 |
从空间一点P向二面角α-1-β的两个平面作垂线PE,PF,E,F为垂足,若∠EPF=60°,则二面角的平面角的大小为( )
| A、60° | B、120° |
| C、60°或120° | D、不确定 |
设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
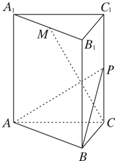 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2