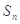题目内容
已知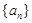 是公差不等于0的等差数列,
是公差不等于0的等差数列,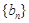 是等比数列
是等比数列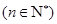 ,且
,且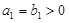 .
.
(1)若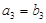 ,比较
,比较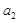 与
与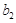 的大小关系;
的大小关系;
(2)若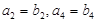 .(ⅰ)判断
.(ⅰ)判断 是否为数列
是否为数列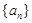 中的某一项,并请说明理由;
中的某一项,并请说明理由;
(ⅱ)若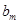 是数列
是数列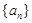 中的某一项,写出正整数
中的某一项,写出正整数 的集合(不必说明理由).
的集合(不必说明理由).
(1)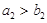 ,(2)
,(2) 是
是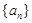 中的一项,正整数
中的一项,正整数 的集合是
的集合是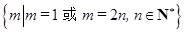 .
.
解析试题分析:(1)记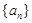 的
的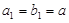 ,
,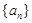 公差为
公差为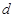 ,
,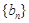 公比为
公比为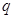 ,由
,由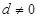 ,得
,得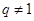 ,比较
,比较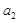 与
与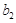 的大小关系,由已知
的大小关系,由已知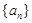 是公差不等于0的等差数列,
是公差不等于0的等差数列,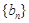 是等比数列
是等比数列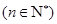 ,且
,且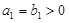 ,且
,且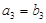 ,得
,得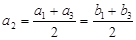 ,
,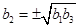 ,当
,当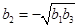 时,显然
时,显然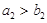 ,当
,当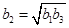 时,由平均值不等式
时,由平均值不等式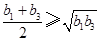 ,从而可比较
,从而可比较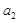 与
与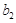 的大小关系;(2)若
的大小关系;(2)若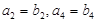 ,可得
,可得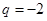 ,
,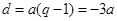 ,(ⅰ)令
,(ⅰ)令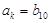 ,由等差数列,等比数列的通项公式,建立方程,解出
,由等差数列,等比数列的通项公式,建立方程,解出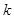 ,若是正整数,
,若是正整数, 为数列
为数列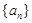 中的某一项,若不是正整数,
中的某一项,若不是正整数, 不是数列
不是数列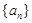 中的一项,(ⅱ)若
中的一项,(ⅱ)若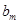 是数列
是数列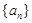 中的某一项,写出正整数
中的某一项,写出正整数 的集合,可由(ⅰ)的方法写出.
的集合,可由(ⅰ)的方法写出.
试题解析:记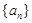 的
的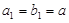 ,
,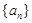 公差为
公差为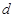 ,
,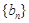 公比为
公比为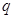 ,由
,由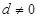 ,得
,得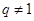
(1)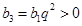 ,
,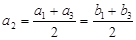 ,
,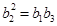 ,
,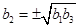 ,
,
当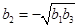 时,显然
时,显然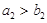 ;
;
当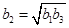 时,由平均值不等式
时,由平均值不等式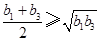 ,当且仅当
,当且仅当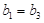 时取等号,而
时取等号,而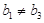 ,所以
,所以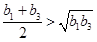 即
即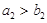 .综上所述,
.综上所述,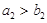 . 5分
. 5分
(2)(ⅰ)因为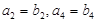 ,所以
,所以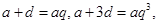 得
得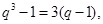 所以
所以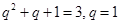 或
或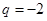 .因为
.因为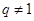 ,所以
,所以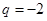 ,
,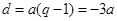 .
.
令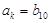 ,即
,即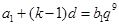 ,
,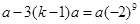 ,
,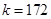 ,所以
,所以 是
是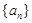 中的一项.
中的一项.
(ⅱ)假设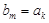

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 的公差
的公差 大于0,
大于0, 是方程
是方程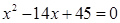 的两根.
的两根.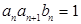 ,求数列
,求数列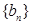 的前
的前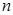 项和.
项和. 的首项
的首项 ,公差
,公差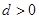 ,且
,且 、
、 、
、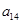 分别是等比数列
分别是等比数列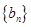 的
的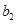 、
、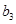 、
、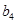 .
.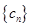 对任意正整数
对任意正整数 均有
均有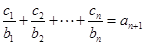 成立,求
成立,求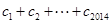 的值.
的值.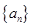 是首项为
是首项为 ,公比
,公比 的等比数列,设
的等比数列,设 .
.
 的前n项和
的前n项和 ;
;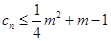 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.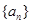 是公比大于
是公比大于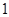 的等比数列,
的等比数列,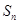 为数列
为数列 项和.已知
项和.已知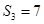 ,且
,且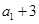 ,
,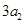 ,
,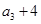 构成等差数列.
构成等差数列.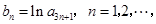 求数列
求数列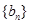 的前
的前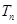 .
.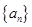 为等差数列,且
为等差数列,且 .
.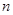 项和为
项和为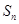 ,若
,若 成等比数列,求正整数
成等比数列,求正整数 的值.
的值.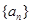 是公差不为0的等差数列,
是公差不为0的等差数列,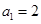 ,且
,且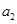 ,
,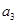 ,
, 成等比数列.
成等比数列.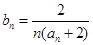 ,求数列
,求数列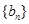 的前
的前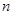 项和
项和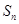 。
。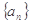 中,
中, 为常数,
为常数,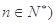 ,且
,且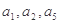 成公比不等于1的等比数列
成公比不等于1的等比数列 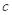 的值;
的值; ,求数列
,求数列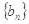 的前
的前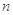 项和
项和