题目内容
已知各项均为正数的数列{an}的前n项和满足Sn>1,且6Sn=(an+1)(an+2),n∈N*.求{an}的通项公式.
an=3n-1
解析解:由a1=S1= (a1+1)(a1+2),
(a1+1)(a1+2),
解得a1=1或a1=2,由已知a1=S1>1,因此a1=2.
又由an+1=Sn+1-Sn= (an+1+1)(an+1+2)-
(an+1+1)(an+1+2)-  (an+1)(an+2),
(an+1)(an+2),
得(an+1+an)(an+1-an-3)=0,
因为an>0,所以an+1-an-3=0.
即an+1-an=3,从而{an}是公差为3,首项为2的等差数列,故{an}的通项为an=3n-1.

练习册系列答案
相关题目
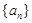 是公差不等于0的等差数列,
是公差不等于0的等差数列,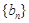 是等比数列
是等比数列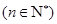 ,且
,且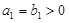 .
.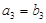 ,比较
,比较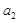 与
与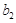 的大小关系;
的大小关系;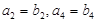 .(ⅰ)判断
.(ⅰ)判断 是否为数列
是否为数列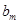 是数列
是数列 的集合(不必说明理由).
的集合(不必说明理由).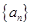 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项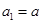 ,
,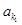 、
、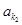 、 、
、 、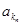 恰为等比数列,且
恰为等比数列,且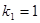 ,
,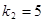 ,
,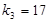 .
.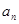 (用
(用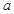 表示);
表示);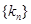 的前
的前 项和为
项和为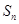 , 求证:
, 求证: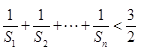 (
(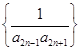 的前n项和.
的前n项和.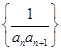 的前n项和,若Tn≤
的前n项和,若Tn≤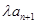 ¨对
¨对 恒成立,求实数
恒成立,求实数 的最小值.
的最小值. ,求数列{bn}的最小值项.
,求数列{bn}的最小值项.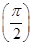 =0.
=0. ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.