题目内容
【题目】已知函数
，其图象与
轴相邻的两个交点的距离为
.
（1）求函数
的解析式；
（2）若将的图象向左平移
个长度单位得到函数
的图象恰好经过点
，求当
取得最小值时，在
上的单调区间.
【答案】（1）
（2）单调增区间为
，
；单调减区间为
.
【解析】
（1）利用两角差的正弦公式，降幂公式以及辅助角公式化简函数解析式，根据其图象与
轴相邻的两个交点的距离为
，得出周期，利用周期公式得出
，即可得出该函数的解析式；
（2）根据平移变换得出
，再由函数
的图象经过点
，结合正弦函数的性质得出
的最小值，进而得出
，利用整体法结合正弦函数的单调性得出该函数在
上的单调区间.
解：（1）
由已知函数
的周期
，
，
∴
.
（2）将的图象向左平移
个长度单位得到的图象
∴，
∵函数的图象经过点
∴
，即
∴
，
∴
，
∵
，∴当
，取最小值，此时最小值为
此时，.
令
，则
当
或
，即当
或
时，函数单调递增
当
，即
时，函数单调递减.
∴在上的单调增区间为
，
；单调减区间为
.
学练快车道口算心算速算天天练系列答案
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．
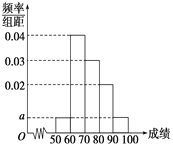
(1)求图中a的值；
(2)根据频率分布直方图，估计这100名学生语文成绩的平均分；
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
【题目】某班同学利用国庆节假期进行社会实践，在
年龄段的人群中随机抽取
人进行了一次生活习惯是否符合低碳观念的调查，生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数的频率分布直方图：
组别 | 分组 | “低碳族”的人数 | 占本组的频率 |
第1组 |
| 120 | 0.6 |
第2组 |
| 195 |
|
第3组 |
| 100 | 0.5 |
第4组 |
|
| 0.4 |
第5组 |
| 30 | 0.3 |
第6组 |
| 15 | 0.3 |
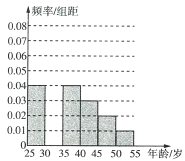
（1）补全频率分布直方图，并求，
，
的值；
（2）从
年龄段的“低碳族”中采用分层随机抽样的方法抽取6人，求从
年龄段的“低碳族”中应抽取的人数.
