题目内容
【题目】问:有多少种不同的方法将集合![]() 中的元素归入
中的元素归入![]() 三个(有序)集合,使得每个元素至少含于其中一个集合之中,这三个集合的交是空集,而其中任两个集合的交都不是空集?
三个(有序)集合,使得每个元素至少含于其中一个集合之中,这三个集合的交是空集,而其中任两个集合的交都不是空集?
【答案】1230
【解析】
如图2,考虑韦恩图所分成的七个部分,分别用![]() 表示.
表示.
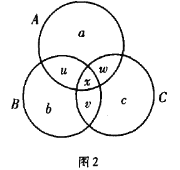
现将![]() 的元素填入各个部分中,由题意,知
的元素填入各个部分中,由题意,知![]() 处不能填数,而
处不能填数,而![]() 处必须填有数字,且所填元素互不相同(否则,相同元素将归入
处必须填有数字,且所填元素互不相同(否则,相同元素将归入![]() 区域中);
区域中);![]() 处可以填或不填数字,不同的区域中不再填有相同元素(否则,又将归入
处可以填或不填数字,不同的区域中不再填有相同元素(否则,又将归入![]() 中).
中).
用![]() 表示
表示![]() 处所填数字的个数,下同.
处所填数字的个数,下同.
由对称性,不妨按![]() 情形列举,则有四种情形:
情形列举,则有四种情形:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() .
.
对于情形(1),从![]() 中各取一数分别置于
中各取一数分别置于![]() 格,有
格,有![]() 种方法,剩下两数各随意放入
种方法,剩下两数各随意放入![]() 格,共有
格,共有![]() 种方法.于是,情形(1)有
种方法.于是,情形(1)有![]() 种.
种.
对于情形(2)中的![]() ,含两个数的格有三种情形,对于其中任一情形,
,含两个数的格有三种情形,对于其中任一情形,![]() 中取两数放入一格,另外两格各放一数,有
中取两数放入一格,另外两格各放一数,有![]() 种,剩下一数放于
种,剩下一数放于![]() 格之一,有3种方法.于是,情形(2)有
格之一,有3种方法.于是,情形(2)有![]() 种.
种.
对于情形(3)中的![]() ,含一个数的格有三种情形,对于其中任一情形,
,含一个数的格有三种情形,对于其中任一情形,![]() 中取一数放入一格,另外取两数放入一格,剩下两数放入另一格,有
中取一数放入一格,另外取两数放入一格,剩下两数放入另一格,有![]() 种.于是,情形(3)有
种.于是,情形(3)有![]() 种.
种.
对于情形(4)中的![]() ,含三个数的格有三种情形,对任一情形,
,含三个数的格有三种情形,对任一情形,![]() 中取三个数放入一格,另外的两格各放一个数,有
中取三个数放入一格,另外的两格各放一个数,有![]() 种.于是,情形(4)有
种.于是,情形(4)有![]() 种.
种.
综上,共有![]() (种).
(种).

练习册系列答案
相关题目
【题目】某校高三年级有500名学生,为了了解数学学科的学习情况,现随机抽出若干名学生在一次测试中的数学成绩(满分150分),制成如下频率分布表:
分组 | 频数 | 频率 |
| ① | ② |
| 0.050 | |
| 0.200 | |
| 12 | 0.300 |
| 0.275 | |
| 4 | ③ |
| 0.050 | |
合计 | ④ |
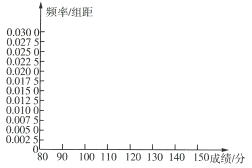
(1)①②③④处应分别填什么?
(2)根据频率分布表完成频率分布直方图.
(3)试估计该校高三年级在这次测试中数学成绩的平均分.


