题目内容
【题目】给定数列![]() ,若满足
,若满足![]() (
(![]() 且
且![]() ),对于任意
),对于任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为指数数列.
为指数数列.
(1)已知数列![]() 、
、![]() 的通项公式分别为
的通项公式分别为![]() ,
,![]() ,试判断
,试判断![]() 、
、![]() 是不是指数数列(需说明理由);
是不是指数数列(需说明理由);
(2)若数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() 是指数数列;
是指数数列;
(3)若![]() 是指数数列,
是指数数列,![]() ,证明:数列
,证明:数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
【答案】(1)![]() 不是指数数列,
不是指数数列,![]() 是指数数列,见解析;(2)见解析;(3)见解析
是指数数列,见解析;(2)见解析;(3)见解析
【解析】
(1)对数列![]() 、
、![]() ,验证
,验证![]() 与
与![]() ,
,![]() 与
与![]() 是否相等,由此判断出
是否相等,由此判断出![]() 、
、![]() 是不是指数数列.
是不是指数数列.
(2)利用累加法求得数列![]() 的通项公式,然后验证
的通项公式,然后验证![]() ,由此证得
,由此证得![]() 是指数数列.
是指数数列.
(3)首先根据指数数列的定义求得数列![]() 的通项公式,利用反证法,证得数列
的通项公式,利用反证法,证得数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
(1)对于数列![]() ,
,![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() 不是指数数列.
不是指数数列.
对于数列![]() ,对任意
,对任意![]() ,因为
,因为![]() ,所以
,所以![]() 是指数数列.
是指数数列.
(2)由题意,![]() ,所以数列
,所以数列![]() 是首项为
是首项为![]() ,公比为2的等比数列.所以
,公比为2的等比数列.所以![]() .
.
所以,![]()
![]() ,
,
即![]() 的通项公式为
的通项公式为![]() .所以
.所以![]() ,故
,故![]() 是指数数列.
是指数数列.
(3)因为数列![]() 是指数数列,故对于任意的
是指数数列,故对于任意的![]() ,有
,有![]() ,令
,令![]() ,则
,则![]() ,
,
所以![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,所以,
的等比数列,所以,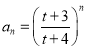 .
.
假设数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() 构成等差数列,不妨设
构成等差数列,不妨设![]() ,
,
则由![]() ,得
,得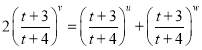 ,所以
,所以![]() ,
,
当![]() 为偶数时,
为偶数时,![]() 是偶数,而
是偶数,而![]() 是偶数,
是偶数,![]() 是奇数,
是奇数,
故![]() 不能成立;
不能成立;
当![]() 为奇数时,
为奇数时,![]() 是偶数,而
是偶数,而![]() 是奇数,
是奇数,![]() 是偶数,
是偶数,
故![]() 也不能成立.
也不能成立.
所以,对任意![]() ,
,![]() 不能成立,
不能成立,
即数列![]() 的任意三项都不成构成等差数列.
的任意三项都不成构成等差数列.
(另证:因为对任意![]() ,
,![]() 一定是偶数,而
一定是偶数,而![]() 与
与![]() 为一奇一偶,故
为一奇一偶,故![]() 与
与![]() 也为一奇一偶,故等式右边一定是奇数,等式不能成立.)
也为一奇一偶,故等式右边一定是奇数,等式不能成立.)

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目