题目内容
3.已知定义域为R的函数f(x)=$\frac{-{2}^{x}+n}{{2}^{x+1}+m}$是奇函数.(Ⅰ)求实数m,n的值;
(Ⅱ)若任意的t∈[-1,1],不等式f(t2-a)+f(at-2)≥0恒成立,求实数a的取值范围.
分析 (1)利用奇函数的性质:过原点,f(-x)=-f(x)代入求得m,n的值;
(2)利用奇函数的性质和单调性得出f(t2-a)≥f(2-at),由二次函数的性质得出满足a的范围,进而求出a的范围.
解答 (本小题满分12分)
解:(Ⅰ)∵f(x)是奇函数,∴f(0)=0,
即$\frac{n-1}{m+2}$=0解得n=1.
f(x)=$\frac{1-{2}^{x}}{m+{2}^{x+1}}$
又由f(1)=f(-1)知$\frac{1-2}{m+4}=-\frac{\frac{1}{2}}{m+1}$
解得m=2…(4分)
经检验,m=2,n=1…(5分)
(2)由(1)知f(x)=$\frac{1-2x}{2+2x+1}$,f(x)在(-∞,+∞)上为减函数.
又∵f(x)是奇函数,∴f(t2-a)≥-f(at-2)
即f(t2-a)≥f(2-at)
∵f(x)为减函数,得t2-a≤2-at.
即任意的t∈[-1,1],有t2-a+at-2≤0.
∴$\left\{\begin{array}{l}f′(1)=1+a-a-2≤0\\ f′(-1)=1-a-a-2≤0\end{array}$,可得a≥-$\frac{1}{2}$.
点评 考察了奇函数的性质和二次函数的性质,属于常规题型,应熟练掌握.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
11.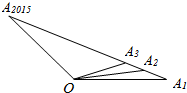 如图,O为直线A1A2015外一点,若A1,A2,A3,A4,A5…A2015中任意相邻两点的距离相等,设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$,其结果为( )
如图,O为直线A1A2015外一点,若A1,A2,A3,A4,A5…A2015中任意相邻两点的距离相等,设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$,其结果为( )
 如图,O为直线A1A2015外一点,若A1,A2,A3,A4,A5…A2015中任意相邻两点的距离相等,设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$,其结果为( )
如图,O为直线A1A2015外一点,若A1,A2,A3,A4,A5…A2015中任意相邻两点的距离相等,设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$,其结果为( )| A. | 2014($\overrightarrow{a}+\overrightarrow{b}$) | B. | 2015($\overrightarrow{a}+\overrightarrow{b}$) | C. | $\frac{2014}{2}$($\overrightarrow{a}+\overrightarrow{b}$) | D. | $\frac{2015}{2}$($\overrightarrow{a}+\overrightarrow{b}$) |
8.已知a,b是实数,命题p:“a+b>5”,命题q:“$\left\{\begin{array}{l}{a>2}\\{b>3}\end{array}\right.$”,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
12.复数z满足(1+i)z=2i(i为虚数单位),则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在平行四边形ABCD中,∠BAD=120°,AB=2,AD=1,若$\overrightarrow{DE}=t\overrightarrow{DC}$,AE⊥BD,则实数t的值为$\frac{2}{5}$.
如图,在平行四边形ABCD中,∠BAD=120°,AB=2,AD=1,若$\overrightarrow{DE}=t\overrightarrow{DC}$,AE⊥BD,则实数t的值为$\frac{2}{5}$.