题目内容
(2013•营口二模)已知椭圆
+
=1的上、下焦点分别为F2和F1,点A(1,-3),
(1)在椭圆上有一点M,使|F2M|+|MA|的值最小,求最小值;
(2)当|F2M|+|MA|取最小值时,求三角形AMF2的周长.
| y2 |
| 25 |
| x2 |
| 9 |
(1)在椭圆上有一点M,使|F2M|+|MA|的值最小,求最小值;
(2)当|F2M|+|MA|取最小值时,求三角形AMF2的周长.
分析:(1)利用椭圆的定义表示出|MF1|+|MF2|,利用三点共线求出|F2M|+|MA|的最小值,以及取得最小值时的条件;
(2)当|F2M|+|MA|取最小值时,此时M、A、F1共线.结合椭圆的定义及两点间的距离公式,从而三角形AMF2的周长.
(2)当|F2M|+|MA|取最小值时,此时M、A、F1共线.结合椭圆的定义及两点间的距离公式,从而三角形AMF2的周长.
解答: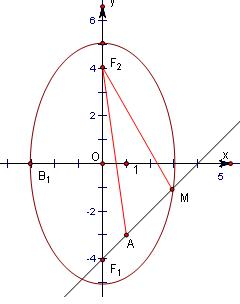 解:(1)如图,椭圆
解:(1)如图,椭圆
+
=1的a=5,b=3,c=4.F2(0,4),F2(0,4),
|AF1|=
,M是椭圆上任一点,由|MF1|+|MF2|=2a=10,
∴|F2M|+|MA|≥2a-|MF1|+|MA|=10-(|MF1|-|MA|)≥10-|AF1|≥10-
,
等号仅当|MF1|-|MA|=|AF1|时成立,此时M、A、F1共线.
∴|F2M|+|MA|的值最小值为10-
,
(2)当|F2M|+|MA|取最小值时,此时M、A、F1共线.
三角形AMF2的周长:
l=|MF2|+|MA|+|AF2|=|MF2|+|MF1|-|MA|+|AF2|
=10-
+5
=10-4
.
 解:(1)如图,椭圆
解:(1)如图,椭圆| y2 |
| 25 |
| x2 |
| 9 |
|AF1|=
| 2 |
∴|F2M|+|MA|≥2a-|MF1|+|MA|=10-(|MF1|-|MA|)≥10-|AF1|≥10-
| 2 |
等号仅当|MF1|-|MA|=|AF1|时成立,此时M、A、F1共线.
∴|F2M|+|MA|的值最小值为10-
| 2 |
(2)当|F2M|+|MA|取最小值时,此时M、A、F1共线.
三角形AMF2的周长:
l=|MF2|+|MA|+|AF2|=|MF2|+|MF1|-|MA|+|AF2|
=10-
| 2 |
| 2 |
| 2 |
点评:本题考查椭圆的定义及定义的应用,表达式的几何意义的应用,考查转化思想与计算能力.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 (2013•营口二模)(几何证明选讲选做题)如图所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则∠DAC=
(2013•营口二模)(几何证明选讲选做题)如图所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则∠DAC=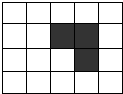 (2013•营口二模)如图所示的阴影部分由方格之上3个小方格组成,我们称这样的图案为L形(每次旋转900仍为L形的图案),那么在4×5个小方格组成的方格纸上可以画出不同位置的L形图案的个数是( )
(2013•营口二模)如图所示的阴影部分由方格之上3个小方格组成,我们称这样的图案为L形(每次旋转900仍为L形的图案),那么在4×5个小方格组成的方格纸上可以画出不同位置的L形图案的个数是( )