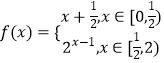题目内容
【题目】近年来，我国许多省市雾霾天气频发，为增强市民的环境保护意识，某市面向全市征召n名义务宣传志愿者，成立环境保护宣传组织
现把该组织的成员按年龄分成5组：第1组
，第2组
，第3组
，第4组
，第5组
，得到的频率分布直方图如图所示，已知第2组有70人．
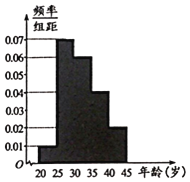
（1）求该组织的人数．
（2）若从第3，4，5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动，然后在这6名志愿者中随机抽取2名志愿者介绍宣传经验，求第3组至少有一名志愿者被抽中的概率．
【答案】（1）
人；（2）
.
【解析】
根据频数
频率
样本容量，频率对应矩形面积，构造关于n的方程，解方程可得该组织的人数；
先计算出第3，4，5组中每组的人数，选求出这6名志愿者中随机抽取2名志愿者的基本事件总数和第3组至少有一名志愿者被抽中的基本事件个数，代入古典概型概率计算公式，可得答案．
由题意：第2组的人数：
，得到：
，
故该组织有200人
第3组的人数为
，
第4组的人数为
，
第5组的人数为
．
第3，4，5组共有60名志愿者，
利用分层抽样的方法在60名志愿者中抽取6名志愿者，每组抽取的人数分别为：
第3组：
；第4组：
；第5组：
．
应从第3，4，5组中分别抽取3人，2人，1人
记第3组的3名志愿者为
，
，
，第4组的2名志愿者为
，第5组的1名志愿者为
．
则从6名志愿者中抽取2名志愿者有：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共有15种．
其中第3组的3名志愿者，，，至少有一名志愿者被抽中的有：
，，，，，，
，，，，，，共有12种，
则第3组至少有一名志愿者被抽中的概率为
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】2012年中华人民共和国环境保护部批准《环境空气质量标准》为国家环境质量标准，该标准增设和调整了颗粒物、二氧化氮、铅、笨等的浓度限值，并从2016年1月1日起在全国实施．空气质量的好坏由空气质量指数确定，空气质量指数越高，代表空气污染越严重，某市对市辖的某两个区加大了对空气质量的治理力度，从2015年11月1日起监测了100天的空气质量指数，并按照空气质量指数划分为：指标小于或等于115为通过，并引进项目投资．大于115为未通过，并进行治理．现统计如下．
空气质量指数 | （0，35] | [35，75] | （75，115] | （115，150] | （150，250] | ＞250 |
空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲区天数 | 13 | 20 | 42 | 20 | 3 | 2 |
乙区天数 | 8 | 32 | 40 | 16 | 2 | 2 |
（1）以频率值作为概率值，求甲区和乙区通过监测的概率；
（2）对于甲区，若通过，引进项目可增加税收40（百万元），若没通过监测，则治理花费5（百万元）；对于乙，若通过，引进项目可增加税收50（百万元），若没通过监测，则治理花费10（百万元）．．在（1）的前提下，记X为通过监测，引进项目增加的税收总额，求随机变量X的分布列和数学期望．
