题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,PA=AC=2,E是PC的中点,∠DAC=∠AOB 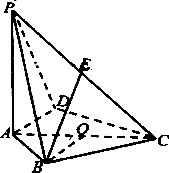
(1)求证:BE∥平面PAD;
(2)若二面角P﹣CD﹣A的正切值为2,求直线PB与平面PCD所成角的正弦值.
【答案】
(1)证明:∵,∠DAC=∠AOB
∴AD∥OB,
∵E是PC的中点,O是AC的中点,
∴OE是△PAC的中位线,
∴OE∥PA,
∵PA∩AD=A,
平面OBE∥平面PAD,
∵BE平面PAD,BE平面PAD,
∴BE∥平面PAD
(2)解:∵AC是圆O的一条直径,∴AC⊥AD,
∵PA⊥平面ABCD,∴PA⊥CD,
则CD⊥平面PAD,
则CD⊥PD,
则∠PDA是二面角P﹣CD﹣A的平面角,
若二面角P﹣CD﹣A的正切值为2,
则tan∠PDA= ![]() =2,
=2,
即AD=1,
建立以D为坐标原点,DA,DC,垂直于平面ABCD的直线分别为x,y,z轴的空间直角坐标系如图:
则B( ![]() ,
, ![]() ,0),P(1,0,2),
,0),P(1,0,2), ![]() =(-
=(- ![]() ,﹣
,﹣ ![]() ,2)
,2)
D(0,0,0),C(0, ![]() ,0),
,0),
则 ![]() =(0,
=(0, ![]() ,0),
,0), ![]() =(1,0,2),
=(1,0,2),
设平面PCD的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 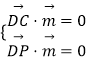 ,即
,即 ![]() ,令z=1,则x=﹣2,y=0,
,令z=1,则x=﹣2,y=0,
即 ![]() =(﹣2,0,1),
=(﹣2,0,1),
则直线PB与平面PCD所成角的正弦值sin< ![]() ,
, ![]() >=|cos<
>=|cos< ![]() ,
, ![]() >|=|
>|=| 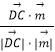 |=
|= ![]()
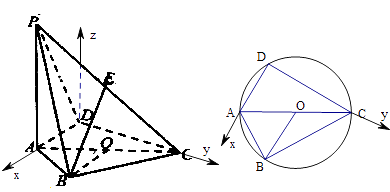
【解析】(1)根据面面平行的性质定理证明平面OBE∥平面PAD,即可证明BE∥平面PAD;(2)建立空间坐标系,根据二面角P﹣CD﹣A的正切值为2,得到AD=1,然后求出平面的法向量,利用直线和平面所成角的定义即可求直线PB与平面PCD所成角的正弦值
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】甲乙两俱乐部举行乒乓球团体对抗赛.双方约定:
①比赛采取五场三胜制(先赢三场的队伍获得胜利.比赛结束)
②双方各派出三名队员.前三场每位队员各比赛﹣场
已知甲俱乐部派出队员A1、A2 . A3 , 其中A3只参加第三场比赛.另外两名队员A1、A2比赛场次未定:乙俱乐部派出队员B1、B2 . B3 , 其中B1参加第一场与第五场比赛.B2参加第二场与第四场比赛.B3只参加第三场比赛
根据以往的比赛情况.甲俱乐部三名队员对阵乙俱乐部三名队员获胜的概率如表:
A1 | A2 | A3 | |
B1 |
|
|
|
B2 |
|
|
|
B3 |
|
|
|
(1)若甲俱乐部计划以3:0取胜.则应如何安排A1、A2两名队员的出场顺序.使得取胜的概率最大?
(2)若A1参加第一场与第四场比赛,A2参加第二场与第五场比赛,各队员每场比赛的结果互不影响,设本次团体对抗赛比赛的场数为随机变量X,求X的分布列及数学期望E(X)