题目内容
【题目】已知函数 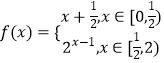 ,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:作出函数的图象:
∵存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2)
∴0≤x1< ![]() ,
,
∵x+ ![]() 在[0,
在[0, ![]() )上的最小值为
)上的最小值为 ![]() ;
;
2x﹣1在[ ![]() ,2)的最小值为
,2)的最小值为 ![]() ,
,
∴x1+ ![]() ≥
≥ ![]() ,x1≥
,x1≥ ![]() ,
,
∴ ![]() ≤x1<
≤x1< ![]() .
.
∵f(x1)=x1+ ![]() ,f(x1)=f(x2)
,f(x1)=f(x2)
∴x1f(x2)﹣f(x2)=x1f(x1)﹣f(x1)2
= ![]() ﹣(x1+
﹣(x1+ ![]() )=x12﹣
)=x12﹣ ![]() x1﹣
x1﹣ ![]() ,
,
设y=x12﹣ ![]() x1﹣
x1﹣ ![]() =(x1﹣
=(x1﹣ ![]() )2﹣
)2﹣ ![]() ,(
,( ![]() ≤x1<
≤x1< ![]() ),
),
则对应抛物线的对称轴为x= ![]() ,
,
∴当x= ![]() 时,y=﹣
时,y=﹣ ![]() ,
,
当x= ![]() 时,y=
时,y= ![]() ,
,
即x1f(x2)﹣f(x2)的取值范围为[﹣ ![]() ,
, ![]() ).
).
故选:B.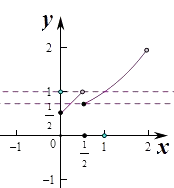

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目