题目内容
2.集合M={x|x=sin$\frac{nπ}{3}$,n∈Z},N={x|x=cos$\frac{nπ}{2}$,n∈N},M∩N等于( )| A. | {-1,0,1} | B. | {0,1} | C. | {0} | D. | {-1,0} |
分析 由M与N,求出两集合的交集即可.
解答 解:∵M={x|x=sin$\frac{nπ}{3}$,n∈Z}={-$\frac{\sqrt{3}}{2}$,0,$\frac{\sqrt{3}}{2}$},
N={x|x=cos$\frac{nπ}{2}$,n∈N}={-1,0,1},
∴M∩N={0},
故选:C.
点评 此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
相关题目
14.已知数列{an}满足a1=0,an+1=an+2n,则a2016等于( )
| A. | 2016×2 017 | B. | 2015×2 016 | C. | 2014×2 015 | D. | 2016×2 016 |
11.以下判断正确的是( )
| A. | “b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件. | |
| B. | 命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” | |
| C. | 命题“在△ABC中,若A>B则sinA>sinB”的逆命题为假命题. | |
| D. | 函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件. |
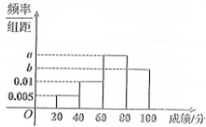 某班的全体学生(共50人)参加数学测试(百分制),成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],依此表可以估计这次测试成绩的中位数为70分.
某班的全体学生(共50人)参加数学测试(百分制),成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],依此表可以估计这次测试成绩的中位数为70分. 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.