题目内容
建造一个容积为8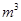 ,深为2
,深为2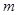 的长方体无盖水池,若池底和池壁的造价每平方米分别为120元和80元,则如何设计此池底才能使水池的总造价最低,并求出最低的总造价.
的长方体无盖水池,若池底和池壁的造价每平方米分别为120元和80元,则如何设计此池底才能使水池的总造价最低,并求出最低的总造价.
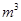 ,深为2
,深为2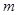 的长方体无盖水池,若池底和池壁的造价每平方米分别为120元和80元,则如何设计此池底才能使水池的总造价最低,并求出最低的总造价.
的长方体无盖水池,若池底和池壁的造价每平方米分别为120元和80元,则如何设计此池底才能使水池的总造价最低,并求出最低的总造价. 解:设池底的一边长为
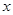 ,另一边长为
,另一边长为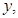 总造价为
总造价为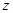 元,依题意有
元,依题意有 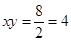
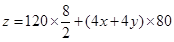
=
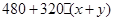


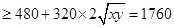
当且仅当
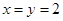 时取等号
时取等号 所以当池底的两边长都为2
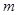 时才能使水池的总造价最低,最低的总造价为1760元.
时才能使水池的总造价最低,最低的总造价为1760元.略

练习册系列答案
相关题目
 ,函数
,函数 若
若 ,则a的值为 ▲ .
,则a的值为 ▲ .
 与
与 ,
, 与
与 ;
; 时,
时, 与
与 有什么关系?并证明你的发现;
有什么关系?并证明你的发现; .
. 年的累计产量为
年的累计产量为 吨,但如果年产量超过
吨,但如果年产量超过 吨,会给环境造成危害.为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是
吨,会给环境造成危害.为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是 是定义在
是定义在 上的奇函数,且
上的奇函数,且 恒成立,当
恒成立,当 时,
时, 则
则 的值为( )
的值为( ) 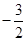



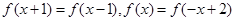 ,方程
,方程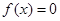 在
在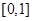 内有且只有一个根
内有且只有一个根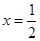 ,则
,则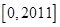 内根的个数为
内根的个数为 



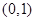 ,否则会出错。
,否则会出错。 的函数
的函数 ,如果存在
,如果存在 ,使得
,使得 成立,称函数
成立,称函数 ”函数。已知下列函数:①
”函数。已知下列函数:① ; ②
; ② ;③
;③ (
( ); ④
); ④ ,其中属于“
,其中属于“ ,垂足为M,
,垂足为M, ,垂足为N,则四边形OMPN的周长的最小值为 .
,垂足为N,则四边形OMPN的周长的最小值为 .
 ,则
,则 = ▲
= ▲