题目内容
14.等差数列{an}中,a2=4,a4+a7=15.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2${\;}^{{a}_{n}-2}$+n,求b1+b2+b3+…+b10的值.
分析 (Ⅰ)建立方程组求出首项与公差,即可求数列{an}的通项公式;
(Ⅱ)bn=2${\;}^{{a}_{n}-2}$+n=2n+n,利用分组求和求b1+b2+b3+…+b10的值.
解答 解:(Ⅰ)设公差为d,则$\left\{\begin{array}{l}{{a}_{1}+d=4}\\{({a}_{1}+3d)+({a}_{1}+6d)=15}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=3}\\{d=1}\end{array}\right.$,
所以an=3+(n-1)=n+2;
(Ⅱ)bn=2${\;}^{{a}_{n}-2}$+n=2n+n,
所以b1+b2+b3+…+b10=(2+1)+(22+2)+…+(210+10)
=(2+22+…+210)+(1+2+…+10)
=$\frac{2(1-{2}^{10})}{1-2}$+$\frac{(1+10)×10}{2}$=2101.
点评 本题考查等差数列的通项,考查数列的求和,求出数列的通项是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
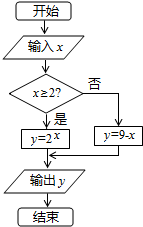
2.阅读如图所示的程序框图,运行相应的程序,若输入x的值为1,则输出y的值为( )

| A. | 2 | B. | 7 | C. | 8 | D. | 128 |
9.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x-4y=0交椭圆E于A,B两点,若|AF|+|BF|=4,点M到直线l的距离不小于$\frac{4}{5}$,则椭圆E的离心率的取值范围是( )
| A. | (0,$\frac{\sqrt{3}}{2}$] | B. | (0,$\frac{3}{4}$] | C. | [$\frac{\sqrt{3}}{2}$,1) | D. | [$\frac{3}{4}$,1) |
6.若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
3.i为虚数单位,i607的共轭复数为( )
| A. | i | B. | -i | C. | 1 | D. | -1 |