题目内容
【题目】已知x2+y2﹣4x﹣2y﹣k=0表示图形为圆.
(1)若已知曲线关于直线x+y﹣4=0的对称圆与直线6x+8y﹣59=0相切,求实数k的值;
(2)若k=15,求过该曲线与直线x﹣2y+5=0的交点,且面积最小的圆的方程.
【答案】
(1)解:已知圆的方程为(x﹣2)2+(y﹣1)2=5+k(k>﹣5),
可知圆心为(2,1),设它关于y=﹣x+4的对称点为(x1,y1),
则 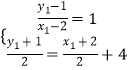 ,解得
,解得 ![]() ,
,
∴点(3,2)到直线6x+8y﹣59=0的距离为 ![]() ,
,
即 ![]()
∴ ![]() ,∴
,∴ ![]()
(2)解:当k=15时,圆的方程为(x﹣2)2+(y﹣1)2=20
设所求圆的圆心坐标为(x0,y0).
∵已知圆的圆心(2,1)到直线x﹣2y+5=0的距离为 ![]() ,
,
则 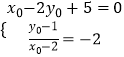 ,∴
,∴ ![]() ,
, ![]() ,
,
∴所求圆的方程为(x﹣1)2+(y﹣3)2=15
【解析】(1)根据两个圆心关于直线对称关系,求出对称圆心的坐标,再由对称圆与6x+8y﹣59=0相切,即圆心到直线的距离等于半径求出圆的半径r,即可求出k;(2)先设圆心A坐标并把k代入已知方程配方后求A的坐标,由A在x﹣2y+5=0上时此圆的面积最小,两个圆心的连线与直线垂直,利用斜率之积等于﹣1和A在直线上列出方程组求圆心的坐标,再利用弦心距、半径和弦的一半关系求出半径.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目